Předpoklad normality závislé proměnné
nezávislý t-test vyžaduje, že závislá proměnná je přibližně normální rozdělení v rámci každé skupiny.
Poznámka: Technicky vzato, je to rezidua, které je třeba být distribuovány normálně, ale pro nezávislý t-test, jak se bude dát stejný výsledek.,
můžete to vyzkoušet pomocí řady různých testů, ale test normality Shapiro-Wilks nebo grafická metoda, jako je graf Q-Q, jsou velmi časté. Tyto testy můžete spustit pomocí statistik SPSS, jejichž postup najdete v našem Průvodci testováním Normality. T-test je však popsán jako robustní test s ohledem na předpoklad normality. To znamená, že určitá odchylka od normality nemá velký vliv na míru chyb typu I. Výjimkou je, pokud je poměr nejmenší k největší velikosti skupiny větší než 1.,5 (Největší ve srovnání s nejmenší).
Co dělat, když porušíte předpokladu normálního rozdělení
Pokud zjistíte, že jeden nebo oba z vaší skupiny nejsou data přibližně normální distribuci a skupiny velikosti se značně liší, máte dvě možnosti: (1) transformovat data tak, že data se stává normálně distribuovaný (k tomu v SPSS Statistiky viz náš průvodce na Transformaci Dat), nebo (2) spusťte Mann-Whitney U test, což je neparametrický test, který nevyžaduje předpoklad normality (ke spuštění tohoto testu v SPSS Statistiky viz náš průvodce na Mann-Whitney U Test).,
Předpoklad homogenity rozptylu
nezávislý t-test předpokládá, že rozptyly obou skupin se měření jsou stejné v populaci. Pokud jsou vaše odchylky nerovnoměrné, může to ovlivnit chybovost typu I. Předpoklad homogenity rozptylu mohou být testovány pomocí Levene ‚ s Test Rovnosti Rozptylů, který je produkován v SPSS Statistics při spuštění nezávislého t-testu., Pokud jste spustili leveneův Test Rovnosti Rozptylů v programu SPSS Statistics, dostanete podobný výsledek jako níže:

Tento test pro homogenitu rozptylu poskytuje F-rozdělení a význam hodnota (p-hodnota). Zabýváme se především významovou hodnotou – pokud je větší než 0,05 (tj. p > .05), naše skupinové odchylky lze považovat za stejné. Pokud však p < 0.05, máme nerovné odchylky a porušili jsme předpoklad homogenity rozptylů.,
Překonání porušení předpokladu homogenity rozptylu
Pokud leveneův Test pro Rovnost Rozptylů je statisticky významný, což naznačuje, že skupina rozptyly jsou rozdílné v populaci, můžete opravit za toto porušení není pomocí sdruženého odhadu pro chybu termín pro t-statistiku, ale místo toho pomocí úpravy stupňů volnosti pomocí Welch-Satterthwaite metoda., Ve skutečnosti, budete pravděpodobně nikdy neslyšel o tyto úpravy, protože SPSS Statistics skrývá tyto informace a jednoduše štítky dvě možnosti, jak „rovností rozptylů převzal“ a „rovností rozptylů není předpokládá, že“ bez výslovně uvede základní testy používané., Nicméně, můžete vidět důkazy, že tyto testy, jak je uvedeno níže:
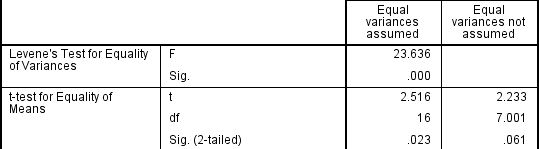
Z výsledku leveneův Test pro Rovnost Rozptylů, můžeme zamítnout nulovou hypotézu, že neexistuje rozdíl v rozptylu mezi skupinami a přijímáme alternativní hypotézu, že existuje statisticky významný rozdíl v rozptylu mezi skupinami., Účinek není schopen předpokládat, rovností rozptylů je patrný v posledním sloupci výše uvedený obrázek, kde vidíme snížení hodnoty t-statistiky a velké snížení stupňů volnosti (df). To má za následek zvýšení hodnoty p nad kritickou úroveň významu 0,05. V tomto případě proto nepřijímáme alternativní hypotézu a akceptujeme, že mezi prostředky neexistují statisticky významné rozdíly. To by nebyl náš závěr, kdybychom netestovali na homogenitu rozptylů.