Úvod
Lineární regrese, také známý jako jednoduchá lineární regrese, nebo se dvěma proměnnými, lineární regrese, se používá, když chceme předpovědět hodnotu závislé proměnné na základě hodnoty nezávislé proměnné. Můžete například použít lineární regresi, abyste pochopili, zda lze výkon zkoušky předvídat na základě doby revize (tj.,, vaše závislá proměnná by byla „výkon zkoušky“, měřeno od 0-100 značek a vaše nezávislá proměnná by byla“ doba revize“, měřeno v hodinách). Střídavě, můžete použít lineární regresi, aby se pochopit, zda se spotřeba cigaret lze předvídat na základě kouření doba trvání (tj. závislou proměnnou bude „spotřeba cigaret“, měřená v počtu cigaret konzumovány denně, a vaše nezávislé proměnné by bylo „kouření doba trvání“, měřeno ve dnech). Pokud máte dvě nebo více nezávislých proměnných, spíše než jen jednu, musíte použít více regresí., Alternativně, pokud si jen přejete zjistit, zda existuje lineární vztah, můžete použít pearsonovu korelaci.
Poznámka: závislá proměnná je také odkazoval se na jako výsledek, cíl nebo kritérium proměnná, zatímco nezávislou proměnnou je také odkazoval se na jako prediktor vysvětlující nebo regressor proměnné. Nakonec, bez ohledu na termín, který používáte, je nejlepší být konzistentní. Budeme se na ně odkazovat jako na závislé a nezávislé proměnné v této příručce.,
v této příručce vám ukážeme, jak provádět lineární regresi pomocí Stata, stejně jako interpretovat a hlásit výsledky tohoto testu. Než vás však seznámíme s tímto postupem, musíte pochopit různé předpoklady, které musí vaše data splňovat, aby vám lineární regrese poskytla platný výsledek. O těchto předpokladech budeme diskutovat dále.
Stata
předpoklady
existuje sedm „předpokladů“, které podporují lineární regresi. Pokud některý z těchto sedmi předpokladů není splněn, nemůžete analyzovat svá data pomocí lineární, protože nebudete mít platný výsledek., Od předpoklady #1 a #2 se týkají vašeho výběru proměnných, nemohou být testovány pomocí Stata. Před pokračováním byste se však měli rozhodnout, zda vaše studie splňuje tyto předpoklady.
- předpoklad #1: Vaše závislá proměnná by měla být měřena na kontinuální úrovni., Příklady takové kontinuální proměnné zahrnují výšku (měří ve stopách a palcích), teplota (měřeno v oC), plat (měřeno v amerických dolarech), revize času (měřeno v hodinách), inteligence (měří pomocí IQ skóre), reakční čas (v milisekundách), test výkonnosti (měřeno od 0 do 100), prodej (měřeno v počtu transakcí za měsíc), a tak dále. Pokud si nejste jisti, zda je vaše závislá proměnná spojitá (tj. měřená na úrovni intervalu nebo poměru), podívejte se na naše typy průvodce proměnnými.,
- předpoklad #2: vaše nezávislá proměnná by měla být měřena na kontinuální nebo kategorické úrovni. Pokud však máte kategorickou nezávislou proměnnou, je častější používat nezávislý t-test (pro 2 skupiny) nebo jednosměrnou ANOVU (pro 3 skupiny nebo více). V případě, že si nejste jisti, příklady kategorické proměnné patří pohlaví (např., 2 skupiny: samec a samice), etnický původ (např. 3 skupin: Běloch, Africký Američan a Hispánské), úroveň fyzické aktivity (např. na 4 skupiny: sedavé, nízké, střední a vysoké) a povolání (např.,, 5 skupin: chirurg, lékař, Zdravotní sestra, zubař, terapeut). V této příručce vám ukážeme lineární regresní postup a výstup Stata, když byly vaše závislé i nezávislé proměnné měřeny na kontinuální úrovni.
naštěstí můžete zkontrolovat předpoklady #3, #4, #5, #6 a # 7 pomocí Stata. Při pohybu na předpoklady #3, #4, #5, #6 a #7, doporučujeme testování je v tomto pořadí, protože to představuje pořadí, kde, pokud porušení předpokladu není opravitelné, nebudete již moci používat lineární regrese., Ve skutečnosti, nebuďte překvapeni, pokud vaše data nesplňuje jednu nebo více z těchto předpokladů, protože je to poměrně typický při práci s real-svět dat, spíše než učebnicové příklady, které se často jen ukazují, jak provádět lineární regrese, když všechno půjde dobře. Nebojte se, protože i když vaše data selže určité předpoklady, často existuje řešení, jak to překonat (např., Jen si pamatujte, že pokud nechcete zkontrolovat, zda data splňuje tyto předpoklady, nebo budete testovat pro ně nesprávně, výsledky dostanete při spuštění lineární regrese nemusí být platná.
- předpoklad #3: musí existovat lineární vztah mezi závislými a nezávislými proměnnými. I když existuje řada způsobů, jak zkontrolovat, zda existuje lineární vztah mezi vašimi dvěma proměnnými, doporučujeme vytvořit scatterplot pomocí Stata, kde můžete vykreslit závislou proměnnou proti vaší nezávislé proměnné., Poté můžete vizuálně zkontrolovat scatterplot a zkontrolovat linearitu. Vaše scatterplot může vypadat podobně jako jednu z následujících akcí:
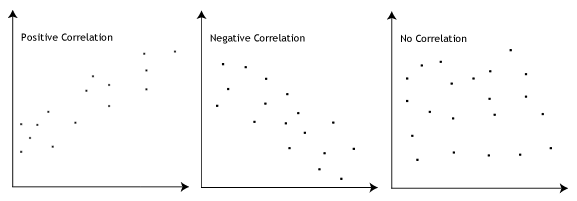
Pokud vztah zobrazeny v scatterplot není lineární, budete muset buď spustit non-lineární regresní analýzy nebo „proměnit“ vaše data, které můžete udělat pomocí Stata.
- předpoklad #4: neměly by existovat žádné významné odlehlé hodnoty. Odlehlé hodnoty jsou jednoduše jednotlivé datové body v rámci vašich dat, které nedodržují obvyklý vzor (např., ve studii z 100 studentů IQ, kde průměrné skóre bylo 108 s jen malými rozdíly mezi studenty, jeden student měl skóre 156, což je velmi neobvyklé, a může dokonce dát ji do top 1% IQ skóre po celém světě). Následující scatterplots upozornit na potenciální vliv odlehlých hodnot:
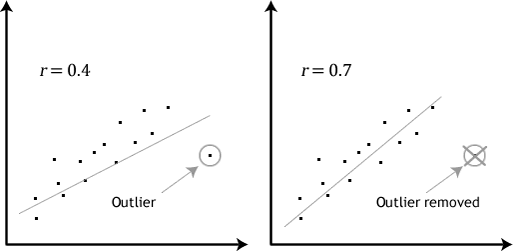
problém odlehlých hodnot je, že mohou mít negativní vliv na regresní rovnice, které se používají k předpovědět hodnotu závislé proměnné na základě nezávislé proměnné., Tím se změní výstup, který Stata produkuje, a sníží se prediktivní přesnost vašich výsledků. Naštěstí můžete použít Stata k provádění diagnostiky casewise, která vám pomůže odhalit možné odlehlé hodnoty.
- Předpoklad #5: měli Byste mít nezávislost pozorování, které si můžete snadno zkontrolovat pomocí Durbin-Watson statistika, což je jednoduchý test spustit pomocí Stata.
- předpoklad #6: Vaše data musí ukázat homoscedasticitu, což je místo, kde odchylky podél linie best fit zůstávají podobné, jak se pohybujete podél linie., Dva scatterplots níže poskytují jednoduché příklady dat, která splňuje tento předpoklad, a ten, který nesplňuje předpoklad:
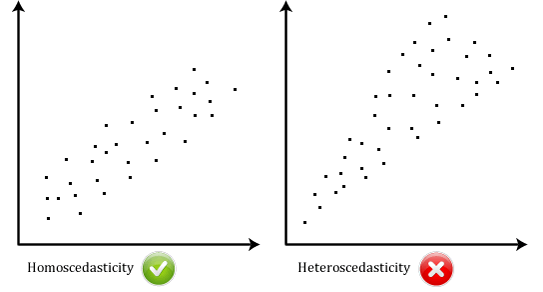
Když budete analyzovat vlastní data, budete mít štěstí, pokud váš scatterplot vypadá to, že jeden ze dvou výše uvedených. Zatímco tyto pomáhají ilustrovat rozdíly v dat, která splňuje nebo porušuje předpoklad homoskedasticity, real-svět dat je často mnohem více chaotický., Můžete zkontrolovat, zda vaše data ukázala, homoskedasticita vynesením regrese standardizovaných reziduí proti regrese standardizovaných předpokládané hodnoty.
- předpoklad #7: nakonec musíte zkontrolovat, zda jsou zbytky (chyby) regresní čáry přibližně normálně distribuovány. Dvě běžné metody pro kontrolu tohoto předpokladu zahrnují použití buď histogramu (s překrývající se normální křivkou) nebo normálního P-P grafu.
v praxi, kontrola předpokladů #3, #4, #5, #6 a #7 pravděpodobně zabere většinu času při provádění lineární regrese., Není to však obtížný úkol a Stata poskytuje všechny nástroje, které k tomu potřebujete.
V sekci postup ilustrujeme postup Stata potřebný k provedení lineární regrese za předpokladu, že nebyly porušeny žádné předpoklady. Nejprve jsme uvedli příklad, který používáme k vysvětlení lineárního regresního postupu ve Stata.
Stata
příklad
studie ukazují, že cvičení může pomoci předcházet srdečním onemocněním. V rozumných mezích, čím více cvičíte, tím menší je riziko, že trpíte srdečními chorobami., Jedním ze způsobů, jak cvičení snižuje riziko srdečních onemocnění, je snížení tuku v krvi, nazývaného cholesterol. Čím více cvičíte, tím nižší je koncentrace cholesterolu. Kromě toho bylo nedávno prokázáno, že množství času, který strávíte sledováním televize – indikátorem sedavého životního stylu – může být dobrým prediktorem srdečních chorob (tj.,
Proto, výzkumník se rozhodli zjistit, zda koncentrace cholesterolu souvisí s čas strávený sledováním TELEVIZE v jinak zdravé 45 na 65 let pro muže (rizikové kategorie lidí). Například, když lidé trávili více času sledováním televize, zvýšila se také jejich koncentrace cholesterolu (pozitivní vztah); nebo se stalo opak? Výzkumník také chtěl znát podíl koncentrace cholesterolu, který by čas strávený sledováním televize mohl vysvětlit, stejně jako schopnost předvídat koncentraci cholesterolu., Výzkumník by pak mohl určit, zda například lidé, kteří strávili osm hodin sledováním televize denně, měli nebezpečně vysokou koncentraci cholesterolu ve srovnání s lidmi, kteří sledovali jen dvě hodiny televize.
k provedení analýzy výzkumný pracovník přijal 100 zdravých mužských účastníků ve věku od 45 do 65 let. Množství času stráveného sledováním televize (tj. nezávislá proměnná, time_tv) a koncentrace cholesterolu (tj. závislá proměnná, cholesterol) byly zaznamenány pro všech 100 účastníků., Vyjádřeno v proměnlivých termínech, výzkumník chtěl regresovat cholesterol včas_tv.
Poznámka: příklad a data použitá pro tuto příručku jsou fiktivní. Právě jsme je vytvořili pro účely této příručky.
Stata
Setup in Stata
Poznámka: nezáleží na tom, zda nejprve vytvoříte závislou nebo nezávislou proměnnou.
po vytvoření těchto dvou proměnných-time_tv a cholesterol-jsme zadali skóre pro každého do dvou sloupců tabulky editoru dat (Edit) (tj., čas v hodinách, že účastníci se dívali na TELEVIZI v levém sloupci (tj. time_tv, nezávislé proměnné), a účastníků koncentrace cholesterolu v mmol/L v pravém sloupci (tj. cholesterol, závislá proměnná), jak je uvedeno níže:
Zveřejněno s písemným souhlasem StataCorp LP.,
Stata
Postup Zkoušky v Stata
V této sekci vám ukážeme, jak analyzovat data pomocí lineární regrese v Stata, kdy šest předpokladů v předchozí části, Předpoklady, nebyly porušeny. Lineární regresi můžete provádět pomocí kódu nebo grafického uživatelského rozhraní Stata (GUI). Po provedení analýzy vám ukážeme, jak interpretovat vaše výsledky. Nejprve zvolte, zda chcete použít kód nebo grafické uživatelské rozhraní Stata (GUI).,
Kód
kód provádět lineární regrese na data má podobu:
regrese DependentVariable IndependentVariable
Tento kód je zapsán do box níže:
Zveřejněno s písemným souhlasem StataCorp LP.,
Pomocí našeho příkladu, kde závislá proměnná je cholesterol a nezávislé proměnné, je time_tv, požadováno kódu bude:
regrese cholesterolu time_tv
Poznámka 1: musíš být přesný při zadávání kódu do box. Kód je „citlivý na velká písmena“. Například pokud jste zadali „Cholesterol“, kde je „C“ spíše velká než malá písmena (tj.,“9fa0ff39b3″ >
Poznámka 2: pokud stále dostáváte chybovou zprávu v poznámce 2: výše, stojí za to zkontrolovat jméno, které jste dali dvěma proměnným v editoru dat při nastavení souboru (tj., V box na pravé straně Data Editor obrazovky, je to tak, že jste napsala svůj proměnných v
oddíl, ne
oddíl, který je třeba zadat do kódu (viz níže pro naše závislá proměnná). To se může zdát zřejmé, ale je to chyba, která je někdy provedena, což má za následek chybu v poznámce 2 výše.
Proto, zadejte kód, regresi cholesterolu time_tv, a stiskněte tlačítko „Return/Enter“ tlačítko na klávesnici.,
Publikováno s písemným souhlasem StataCorp LP.
můžete vidět výstup Stata, který bude vytvořen zde.,
Grafické Uživatelské Rozhraní (GUI)
tři kroky potřebné k provádění lineární regrese v Stata 12 a 13 jsou uvedeny níže:
- Statistiky > Lineární modely a související > Lineární regrese na hlavní menu, jak je uvedeno níže:
Zveřejněno s písemným souhlasem StataCorp LP.,
Ty budou prezentovány s Regrese – Lineární regrese dialogové okno:
Zveřejněno s písemným souhlasem StataCorp LP.
- Vyberte cholesterol z závislé proměnné: rozevírací pole a time_tv z nezávislých proměnných: rozevírací pole. Skončí s následující obrazovka:
Zveřejněno s písemným souhlasem StataCorp LP.,
-
klikněte na tlačítko
. Tím se vygeneruje výstup.
Stata
Výstup lineární regresní analýzy v Stata
Pokud vaše údaje předány předpokladu, #3 (tj., tam byl lineární vztah mezi dvěma proměnnými), #4 (tj., tam byly žádné významné odlehlé hodnoty), předpoklad #5 (tj. měl jsi nezávislost pozorování), předpoklad #6 (tj., vaše data ukázala, homoskedasticita) a předpoklad, #7 (tj.,, rezidua (chyby) byly přibližně normální rozdělení), které jsme si vysvětlili dříve v Předpokladech oddílu, budete potřebovat pouze interpretovat následující lineární regrese výstup v Stata:
Zveřejněno s písemným souhlasem StataCorp LP.,
výstup se skládá ze čtyř důležité informace: (a) R2 hodnota („R-squared“ řádku) vyjadřuje podíl variance v závislé proměnné, které mohou být vysvětleny tím, že naše nezávislé proměnné (technicky je podíl variability připadá na regresní model nad rámec střední model). R2 je však založen na vzorku a je pozitivně zkresleným odhadem podílu rozptylu závislé proměnné účtované regresním modelem (tj., to je příliš velké); (b) upravené R2 hodnota („Adj R-squared“ row), která koriguje pozitivní bias poskytnout hodnotu, která by se očekávat, že v populaci; (c) F hodnota, stupně volnosti („F( 1, 98)“) a statistická významnost regresního modelu („Prob > F“ row); a (d) koeficienty pro konstantní a nezávislá proměnná („Coef.“sloupec), což jsou informace, které potřebujete k předpovědi závislé proměnné, cholesterolu, pomocí nezávislé proměnné, time_tv.
v tomto příkladu R2 = 0.151. Upravený R2 = 0,143 (na 3 d.p.,), což znamená, že nezávislá proměnná, time_tv, vysvětluje 14,3% variability závislé proměnné, cholesterolu, v populaci. Upravené R2 je také odhad velikosti účinku, které na 0.143 (14.3%), svědčí o střední velikost účinku podle Cohena (1988) klasifikace. Obvykle se však jedná o R2, který není upravený R2, který je uveden ve výsledcích. V tomto příkladu je regresní model statisticky významný, F (1, 98) = 17, 47, p = .0001., To naznačuje, že celkově použitý model může statisticky významně předpovědět závislou proměnnou, cholesterol.
Poznámka: výstup z lineární regresní analýzy prezentujeme výše. Nicméně, protože měl jste testovány vaše data předpoklady, které jsme si vysvětlili dříve v Předpokladech, bod, budete také muset interpretovat Stata výstup, který byl produkován při testování těchto předpokladů. To zahrnuje: (a) rozptyl, který jste použili ke kontrole, zda existuje lineární vztah mezi vašimi dvěma proměnnými (tj.,, Předpoklad #3); (b) casewise diagnostics zkontrolovat, tam byly žádné významné odlehlé hodnoty (tj. Předpoklad, #4); (c) výstup z Durbin-Watson statistika pro kontrolu nezávislost pozorování (tj. Předpoklad, #5); (d) scatterplot regrese standardizovaných reziduí proti regrese standardizovaných předpokládaná hodnota k určení, zda vaše data ukázala, homoskedasticita (tj. Předpoklad, #6); a histogram (s položený normální křivky) a Normální P-P grafu zkontrolovat, zda rezidua (chyby) byly přibližně normální rozdělení (tj. Předpoklad, #7)., Také, nezapomeňte, že pokud vaše data nepodařilo žádný z těchto předpokladů, výstup, který dostanete od lineární regrese postup (tj. výstupní jsme diskutovali výše), již nebude relevantní, a možná budete muset provést různé statistické testy analyzovat vaše data.,
Stata
Hlášení výstup lineární regresní analýzy
Když zpráva výstup lineární regrese, je dobré praxe patří: (a) úvod do analýzy, kterou provádí; (b) informace o vzorku, včetně všech chybějících hodnot; (c) pozorované F-hodnotu, počet stupňů volnosti a hladinu významnosti (např. p-hodnoty); (d) procento variability v závislé proměnné je vysvětleno tím, že nezávislá proměnná (tj., vaše Upravené R2 ); a (e) regresní rovnice pro váš model., Na základě výsledků výše uvedené, můžeme výsledky této studie následovně:
- Obecné
lineární regrese zjištěno, že denní doba sledování TELEVIZE by statisticky významně předpovídají, koncentrace cholesterolu, F(1, 98) = 17.47, p = .0001 a čas strávený sledováním TELEVIZE představovaly 14,3% vysvětlované variability koncentrace cholesterolu. Regresní rovnice byla: předpokládaná koncentrace cholesterolu = -2.135 + 0.044 x (čas strávený sledováním televize).,
kromě hlášení výše uvedených výsledků lze diagram použít k vizuálnímu prezentaci vašich výsledků. Můžete to například provést pomocí scatterplotu s intervaly spolehlivosti a predikce (i když není příliš běžné přidávat Poslední). To může ostatním usnadnit pochopení vašich výsledků. Dále můžete použít lineární regresní rovnici k předpovědi o hodnotě závislé proměnné na základě různých hodnot nezávislé proměnné., Zatímco Stata nevytváří tyto hodnoty jako součást výše uvedeného lineárního regresního postupu, ve Stata existuje postup, který můžete použít k tomu.