Jsme klasicky, že světla jako vždy cestují v přímých linkách, ale když se světelné vlny projít blízkosti bariéru, mají tendenci se ohýbat kolem bariéry a stát se rozprostíral. Difrakce světla nastává, když světelná vlna prochází rohem nebo otvorem nebo štěrbinou, která je fyzicky přibližná velikost nebo dokonce menší než vlnová délka tohoto světla.,

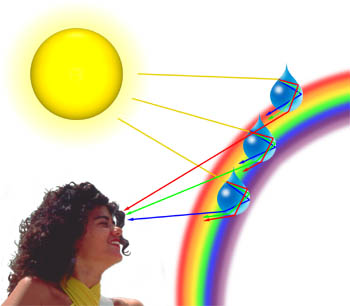
velmi jednoduchá demonstrace difrakce může být provedeno tím, že drží své ruce v přední části světelného zdroje a pomalu uzavírají dva prsty při pozorování světlo přenáší mezi nimi. Jak se prsty přibližují a přicházejí velmi blízko k sobě, začnete vidět řadu tmavých čar rovnoběžných s prsty. Paralelní čáry jsou vlastně difrakční vzory. Tento jev může také nastat, když je světlo „ohnuté“ kolem částic, které jsou ve stejném pořadí jako vlnová délka světla., Dobrým příkladem je difrakce světla mraky, které často označujeme jako klad, je znázorněno na Obrázku 1 s krásný západ slunce nad oceánem.
často můžeme pozorovat pastelové odstíny modré, růžové, fialové a zelené v oblacích, které vznikají, když je světlo rozptýleno z kapiček vody v oblacích. Množství difrakce závisí na vlnové délce světla, s kratší vlnové délky, že difraktovaný na úhel větší než ty delší (v platnosti, modrá a fialová světla difraktovaného na vyšší úhel než je červené světlo)., Jako světelné vlny cestují přes atmosféru setkání kapička vody, jak je znázorněno níže, je nejprve láme na vodu:air rozhraní, pak se odráží, jak to zase narazí na rozhraní. Paprsek, který stále cestuje uvnitř vodní kapky, je opět lomený, když narazí na rozhraní potřetí. Tato poslední interakce s rozhraním odráží světlo zpět do atmosféry, ale také difraktuje část světla, jak je znázorněno níže., Tento difrakční prvek vede k jevu známého jako Cellini je halo (také známý jako Heiligenschein účinek), kde jasný prstenec světla obklopuje stín pozorovatelovy hlavy.
termíny difrakce a rozptyl se často používají zaměnitelně a jsou považovány za téměř synonymní. Difrakce popisuje speciální případ rozptylu světla, ve kterém objekt s pravidelně se opakující rysy (jako difrakční mřížka) produkuje řádné difrakce světla na difrakční obrazec., V reálném světě je většina objektů velmi složitého tvaru a měla by být považována za složenou z mnoha individuálních difrakčních rysů, které mohou společně produkovat náhodný rozptyl světla.
jedním z klasických a nejzákladnějších konceptů zahrnujících difrakci je experiment s optickou difrakcí s jednou štěrbinou, který byl poprvé proveden na počátku devatenáctého století. Když se světelná vlna šíří štěrbinou (nebo clonou), výsledek závisí na fyzické velikosti otvoru vzhledem k vlnové délce dopadajícího paprsku., To je znázorněno na Obrázku 3 za předpokladu, koherentní, monochromatické vlny emitované z bodového zdroje S, podobné světlo, které by bylo vyráběné pomocí laseru, prochází přes clony d a je difraktovaný, s primární dopadající světelný paprsek přistání na bod P a první sekundární maxima, vyskytující se v bodě Q.
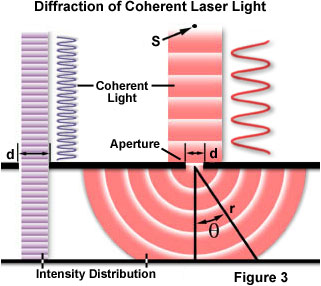
Jak je znázorněno v levé části obrázku, při vlnové délce (λ) je mnohem menší, než je šířka otvoru (d), vlna prostě cestuje kupředu v přímce, stejně jako by to byly částice, nebo ne clony byly přítomny., Nicméně, když vlnová délka přesahuje velikost clony, máme zkušenosti difrakce světla podle rovnice:
Kde θ je úhel mezi incidentu centrální propagace směrem a první minimální difrakční obrazec. Experiment produkuje jasné centrální maximum, které je lemován na obou stranách sekundární maxima, s intenzitou každý následující sekundární maximální snížení jako vzdálenost od středu zvyšuje. Obrázek 4 znázorňuje tento bod se zápletkou intenzity paprsku versus poloměrem difrakce., Všimněte si, že minima vyskytující se mezi sekundárními maximy jsou umístěna v násobcích π.
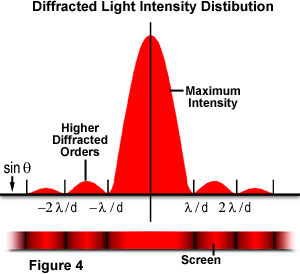
Tento experiment byl poprvé vysvětlil Augustin Fresnel, který, spolu s Thomas Young, vyrobené důležité důkazy potvrzující, že světlo cestuje ve vlnách. Z výše uvedených čísel vidíme, jak koherentní monochromatické světlo (v tomto příkladu laserové osvětlení) vyzařované z bodu L je difraktováno clonou d., Fresnelovy předpokládat, že amplituda prvního řádu maxima v bodě Q (definované jako eQ) by byla dána rovnicí:
kde A je amplituda dopadající vlny, r je vzdálenost mezi d a Q a f(χ) je funkce χ, sklon faktor představen Fresnel.
Difrakce Světla
Prozkoumat, jak paprsek světla je difraktovaného když prochází úzkou štěrbinou nebo otvorem. Upravte velikost vlnové délky a clony a sledujte, jak to ovlivňuje vzor intenzity difrakce.,
difrakce světla hraje prvořadou roli při omezování rozlišovací schopnosti jakéhokoli optického nástroje (například: kamery, dalekohled, dalekohledy, mikroskopy a oko). Rozlišovací schopnost je schopnost optického přístroje vytvářet samostatné obrazy dvou sousedních bodů. To je často určeno kvalitou čoček a zrcadel v přístroji, jakož i vlastnostmi okolního média (obvykle vzduchu). Vlnová povaha světla nutí konečný limit rozlišovací síly všech optických přístrojů.,
naše diskuse o difrakci použily štěrbinu jako otvor, kterým je difraktováno světlo. Všechny optické přístroje však mají kruhové otvory, například zornici oka nebo kruhovou membránu a čočky mikroskopu. Kruhové otvory vytvářejí difrakční vzory podobné těm, které jsou popsány výše, s výjimkou vzoru přirozeně vykazuje kruhovou symetrii. Matematická analýza difrakčních vzorců vytvořených kruhovou clonou je popsána rovnicí:
kde θ(1) je úhlová pozice prvního řádu difrakce minima (první tmavý kroužek), λ je vlnová délka dopadajícího světla, d je průměr clony, a 1.22 je konstantní. Ve většině případů, úhel θ(1) je velmi malý, takže sbližování že sin a tan úhlu jsou téměř stejné výnosy:
Z těchto rovnic je zřejmé, že centrální maximum je přímo úměrná λ/d, takže tato maximální více rozložit na delší vlnové délce a pro menší otvory., Sekundární mimina difrakce stanovila limit užitečného zvětšení objektivních čoček v optické mikroskopii v důsledku inherentní difrakce světla těmito čočkami. Bez ohledu na to, jak dokonalý objektiv, může být obraz bodového zdroje světla produkovaného objektiv je doprovázena sekundární a vyšší řád maxima. To by mohlo být odstraněno pouze v případě, že čočka měla nekonečný průměr. Dva objekty oddělené vzdáleností menší než θ (1) nelze vyřešit, bez ohledu na to, jak vysoký je výkon zvětšení., Zatímco tyto rovnice byly odvozeny pro obraz bodového zdroje světla, nekonečné vzdálenosti od clony, to je přijatelný odhad na rozlišovací schopnost mikroskopu, když d je nahrazen průměrem objektivu.
to Znamená, když dva objekty jsou umístěny vzdálenosti D od sebe a jsou ve vzdálenosti L od pozorovatele, úhel (v radiánech) mezi nimi je:
což nás vede k být schopen kondenzovat poslední dvě rovnice se získá:
kde D (0) je minimální separační vzdálenost mezi objekty, která jim umožní vyřešit. Pomocí této rovnice, lidské oko může vyřešit objekty od sebe vzdáleny 0,056 mm, nicméně fotoreceptory v sítnici nejsou zcela dostatečně blízko, aby umožnily tento stupeň rozlišení, a 0,1 mm je realističtější číslo za normálních okolností.
rozlišovací schopnost optických mikroskopů je určena řadou faktorů, včetně diskutovaných, ale za nejideálnějších okolností je toto číslo asi 0,2 mikrometru., Toto číslo musí brát v úvahu optické zarovnání mikroskopu, kvalitu čoček a převládající vlnové délky světla používané k obrazu vzorku. Zatímco to je často není nutné vypočítat přesnou rozlišovací schopnost každého cíle (a byla by to ztráta času ve většině případů), je důležité pochopit možnosti mikroskop čočky, jako se vztahují na reálný svět.
přispívající autoři
Mortimer Abramowitz-Olympus America, Inc., Dva Firemní Centrum Drive., Melville, New York, 11747.
Michael W., Davidson – National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., Florida State University, Tallahassee, Florida, 32310.