Výsledky Učení
- Identifikovat ohniska, vrcholy, os a středu elipsy.
- napište rovnice elipsy vystředěné na počátku.
- napište rovnice elipsy, které nejsou vystředěny na počátku.
kuželosečka, nebo kuželovitý, je tvar vyplývající z protínajících právo kruhového kužele s rovinou. Úhel, ve kterém rovina protíná kužel, určuje tvar.,
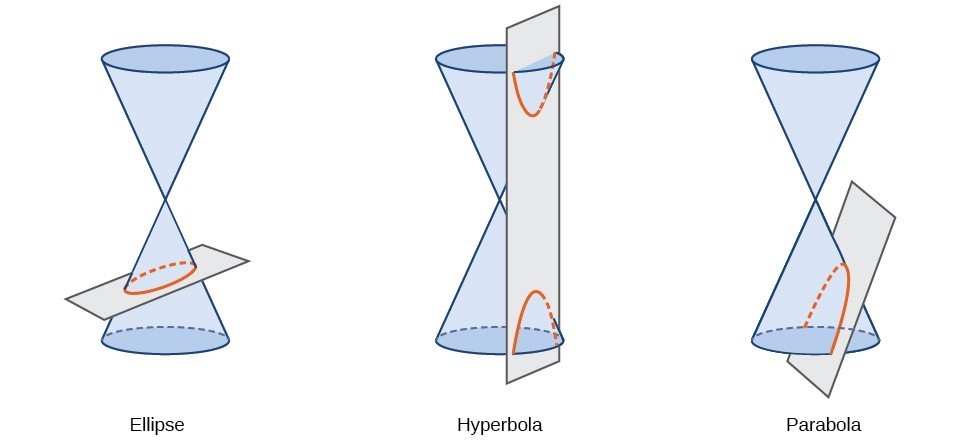
kuželové sekce lze také popsat sadou bodů v rovině souřadnic. Později v této kapitole uvidíme, že graf jakékoli kvadratické rovnice ve dvou proměnných je kuželovitá část. Znaky rovnic a koeficienty proměnných pojmů určují tvar. Tato část se zaměřuje na čtyři varianty standardní formy rovnice pro elipsu. Elipsa je množina všech bodů \ vlevo (x, y \ vpravo) v rovině tak, že součet jejich vzdáleností od dvou pevných bodů je konstantní., Každý pevný bod se nazývá zaostření (množné číslo: ohniska) elipsy.
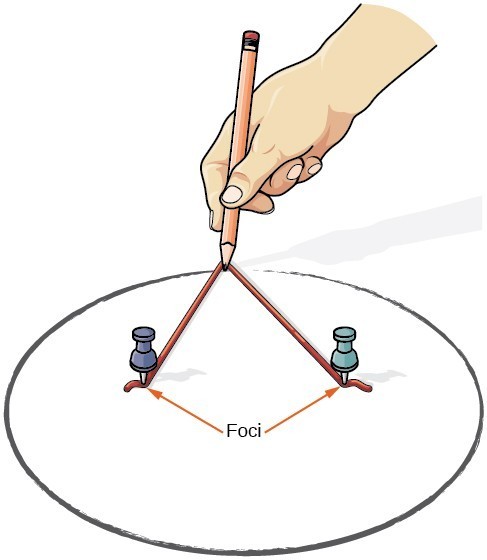
elipsu můžeme nakreslit pomocí kusu lepenky, dvou Paleček, tužky a řetězce. Umístěte palčáky do lepenky a vytvořte ohniska elipsy. Odřízněte kus řetězce delší než vzdálenost mezi oběma palci (délka řetězce představuje konstantu v definici). Připoutejte každý konec řetězce na lepenku a vystopujte křivku tužkou přidrženou napnutou proti řetězci. Výsledkem je elipsa.
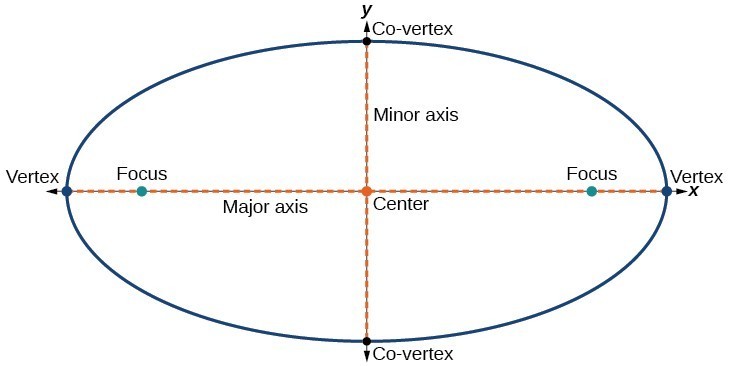
každá elipsa má dvě osy symetrie., Delší osa se nazývá hlavní osa a kratší osa se nazývá menší osa. Každý koncový bod hlavní osy je vrchol elipsy (množné číslo: vrcholy), a každý koncový bod vedlejš osy je co-vrchol elipsy. Střed elipsy je středem hlavních i menších OS. Osy jsou ve středu kolmé. Ložiska vždy leží na hlavní ose a součet vzdáleností od ohnisek do libovolného bodu na elipse (konstantní součet) je větší než vzdálenost mezi ložiska.,
v této sekci omezujeme elipsy na ty, které jsou umístěny svisle nebo vodorovně v rovině souřadnic. To znamená, že osy budou buď ležet nebo budou rovnoběžné s osami x a y. Později v kapitole uvidíme elipsy, které se otáčejí v rovině souřadnic.
práce s horizontální a vertikální elipsy v rovině souřadnic, můžeme uvažovat dva případy: ty, které jsou zaměřené na původ a ty, které jsou zaměřené na jiném místě než na původu., Nejprve se naučíme odvodit rovnice elipsy a pak se naučíme psát rovnice elipsy ve standardní podobě. Později použijeme to, co se naučíme kreslit grafy.,v>, Pokud (x,y) je bod na elipse, pak můžeme definovat následující proměnné:
\begin{align}d_1&=\text{vzdálenost } (-c,0) \text{ k } (x,y) \\ d_2&= \text{vzdálenost } (c,0) \text{ k } (x,y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
pro elipsu na střed v počátku s jeho hlavní osou na ose X a
\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1,
pro elipsu na střed v počátku s jeho hlavní osou na ose Y.,
Psaní Rovnice Elipsy Není vycentrováno na Původ
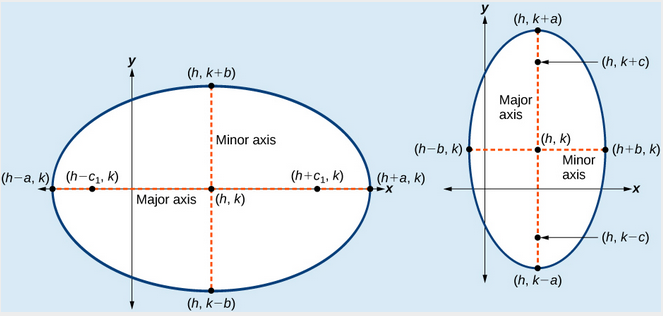
(a) Horizontální elipsa se středem \left(h,k\right) (b) Vertikální elipsy se středem \left(h,k\right)
Řešení Aplikovaných Problémů Týkajících se Elipsy
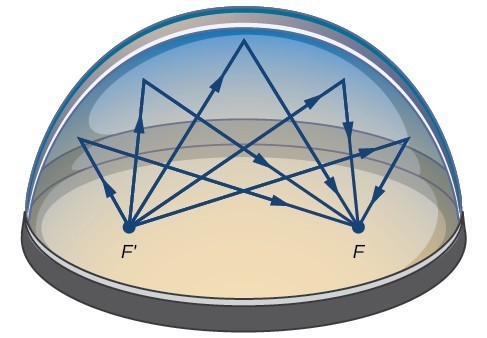
Mnoho reálných situacích může být reprezentován elipsy, včetně oběžné dráhy planet, družic, měsíce a komety, a tvary lodí kýly, kormidla a některých křídla letadla. Lékařské zařízení zvané litotripter používá eliptické reflektory k rozbití ledvinových kamenů generováním zvukových vln., Některé budovy, zvané whispering chambers, jsou navrženy s eliptickými kopulemi, takže člověk šeptající na jednom ohnisku může snadno slyšet někdo stojící na druhém ohnisku. K tomu dochází kvůli akustickým vlastnostem elipsy. Když zvuková vlna vznikne v jednom ohnisku šeptající Komory, zvuková vlna se odrazí od eliptické kupole a zpět do druhého ohniska. V šeptací komoře v Muzeu vědy a průmyslu v Chicagu se dva lidé stojící u ohnisek—asi 43 stop od sebe—mohou navzájem slyšet šepot.