Toto je první ze tří post série. Druhý příspěvek hovoří o tomjak vypočítat Big-o. třetí článek hovoří o pochopeníformální definice big-o.
Big-O notace byla pro mě opravdu děsivá koncepce. Myslel jsem, že takhle“ skuteční “ programátoři mluvili o svém kódu. Bylo to všechno děsivější, protože akademické popisy (například Wikipedie) mi dávaly velmi malý smysl. To je frustrující, protože underlyingconcepts nejsou ve skutečnosti tak těžké.,
jednoduše řečeno, Big – O notace je, jak programátoři mluví oalgorithms. Algoritmy jsou další děsivé téma, které budu krýt v jiném příspěvku, ale pro naše účely, řekněme, že „algoritmus“ se rozumí funkce v programu (což není příliš daleko). Funkce Big-Onotation je určena tím, jak reaguje na různé vstupy. Jakmnohem pomalejší je, když mu dáme seznam 1000 věcí, na kterých je třeba pracovatmísto seznamu 1 věc?
Zvážit tento kód:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
pokud nazýváme tuto funkci jako item_in_list(2, ), to by mělo být docela rychlé., Smyčíme každou věc v seznamu a pokud najdemeprvní argument k naší funkci, vrátit True. Pokud se dostaneme do koncea nenašli jsme to, vraťte se falešně.
„složitost“ této funkce je O(n). Vysvětlím vám, co to znamená za vteřinu, ale pojďme rozebrat tuto matematikusyntax. O(n) se čte“ Order of N“, protože funkce O je také známá jako funkce objednávky. Myslím, že je to proto, že provádímaproximace, která se zabývá „řády“.,
„řády“ je další matematický termín, kterýzákladně říká rozdíl mezi třídami čísel. Myslete na rozdíl mezi 10 a 100. Pokud si představíte 10 svých nejbližších přátel a 100 lidí, je to opravdu velký rozdíl. Podobně rozdíl mezi 1 000 a 10 000 je poměrně velký (ve skutečnosti je to rozdíl mezi vozem junker a lehce použitým). Ukazuje se, že v přibližování,pokud jste v řádu, jste docela blízko., Pokud byste měli odhadnout počet gumballs v amachine, byste být v řádu, pokud jste řekl 200gumballs. 10 000 gumballů by bylo daleko.

Obrázek 1: gumball stroje, jejichž počet gumballs je pravděpodobně v řádově 200.
Zpět na pitevní O(n), to říká, že pokud bychom měli graf timeit trvá na spuštění této funkce s různé velikosti vstupů (např. anarray 1 položky 2 položky 3 položky, atd), tak bychom viděli, že itapproximately odpovídá počtu položek v poli., Jedná se o lineární graf. To znamená, že čára je v podstatě rovnápokud jste ji měli grafovat.
Někteří z vás mohou chytit, že pokud v ukázce kódu výše, ouritem byl vždy první položku v seznamu, náš kód by být reallyfast! To je pravda, ale Big-O je o přibližné nejhorší-případvýkon něco udělat. Nejhorší případ pro výše uvedený kód ježe věc, kterou hledáme, není v seznamu vůbec. (Poznámka: matematický termín pro toto je „horní hranice“, což znamená jeho mluvenímatematický limit awfulness).,
Pokud jste chtěli vidět graf pro tyto funkce, budete ignorovat O()funkce a změnit proměnné n x. Pak můžete zadat, že Wolfram Alpha jako „plot x“, který vám ukáže úhlopříčku. Důvod, proč jste vyměnili n pro x je, že jejich grafy programwants x jak jeho název proměnné, protože to odpovídá xaxis. Osa X, která se zvětšuje zleva doprava, odpovídá velikosti větších a větších polí vaší funkce., Y-axispředstavuje čas, takže čím vyšší je čára, tím pomalejší je.
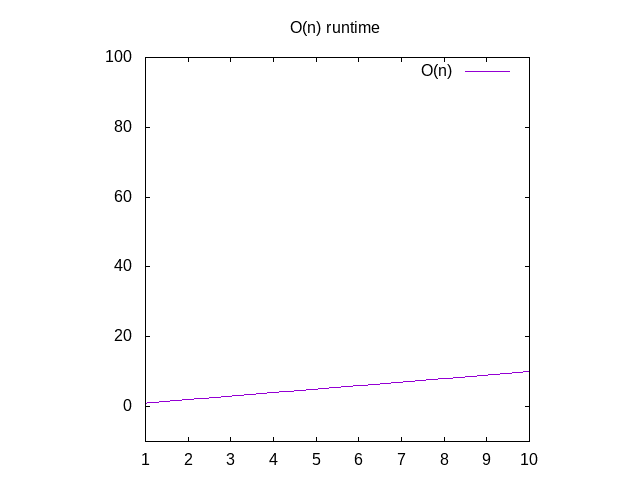
Obrázek 2: Runtime vlastnosti O(n) funkce
jaké jsou další příklady?
zvažte tuto funkci:
def is_none(item): return item is None
Toto je trochu hloupý příklad, ale mějte se mnou. Tato funkce je nazývána O(1), která se nazývá „konstantní čas“. Co to znamená, Je nomatter jak velký je náš vstup, to vždy trvá stejné množství času pro výpočet věci., Pokud se vrátíte do wolframu a plot 1, uvidíte, že to vždy zůstane stejné, bez ohledu na to, jak daleko jdeme. Pokud youpass v seznamu 1 milion celá čísla, to bude trvat asi stejné timeas pokud jste se chystáte projít v seznamu 1 Celé číslo. Konstantní čas jepovažován za nejlepší scénář pro funkci.
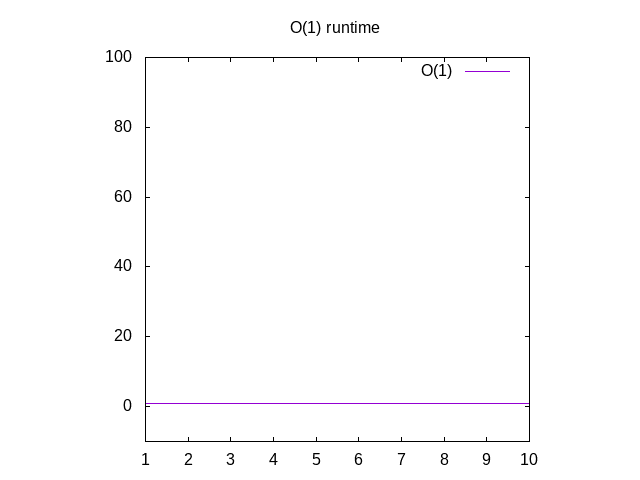
Obrázek 3: Runtime vlastnosti O(1) funkce
Zvážit tyto funkce:
Níže je srovnání jednotlivých grafů, pro referenci., Můžete vidět, že funkce O(n^2) se velmi rychle zpomalí, kde jako něco, co pracuje v konstantním čase, bude mnohem lepší. To je zvláště užitečné, pokud jde o datové struktury, o kterých brzy zveřejním.
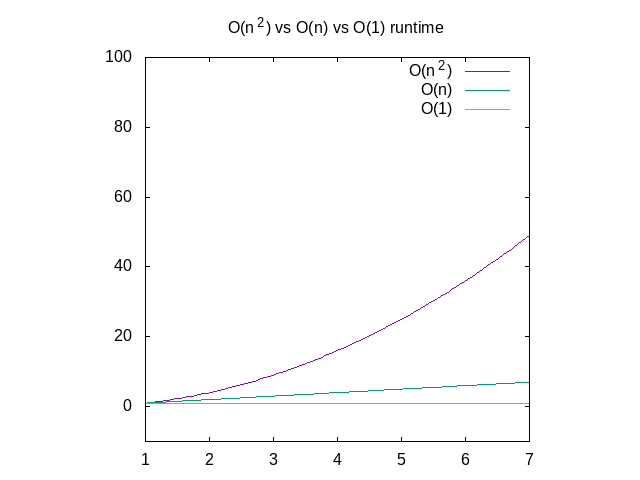
Obrázek 4: Srovnání O(n2) vs O(n) vs O(1) funkce
To je docela vysoké úrovni přehled o tom, Big-O notace, ale hopefullygets vám seznámit se s tématem., Existuje kurz coursera, kterýmůže vám poskytnout podrobnější pohled na toto téma, ale buďte varováni, žeto se dostane do mathematické notace velmi rychle. Pokud něco tady nedává smysl, pošlete mi e-mail.
aktualizace: také jsem psal o tom, jak vypočítat Big-o.
přemýšlím o napsání knihy na toto téma. Pokud je to něco, co byste chtěli vidět, prosím, vyjádřete svůj zájem o to zde.