Lernergebnisse
- Identifizieren Sie die Brennpunkte, Eckpunkte, Achsen und den Mittelpunkt einer Ellipse.
- Schreiben Sie Gleichungen von Ellipsen, die am Ursprung zentriert sind.
- Schreiben Sie Gleichungen von Ellipsen, die nicht am Ursprung zentriert sind.
Ein konischer Abschnitt oder eine konische Form ist eine Form, die sich aus dem Schneiden eines rechten Kreiskegels mit einer Ebene ergibt. Der Winkel, in dem die Ebene den Kegel schneidet, bestimmt die Form.,
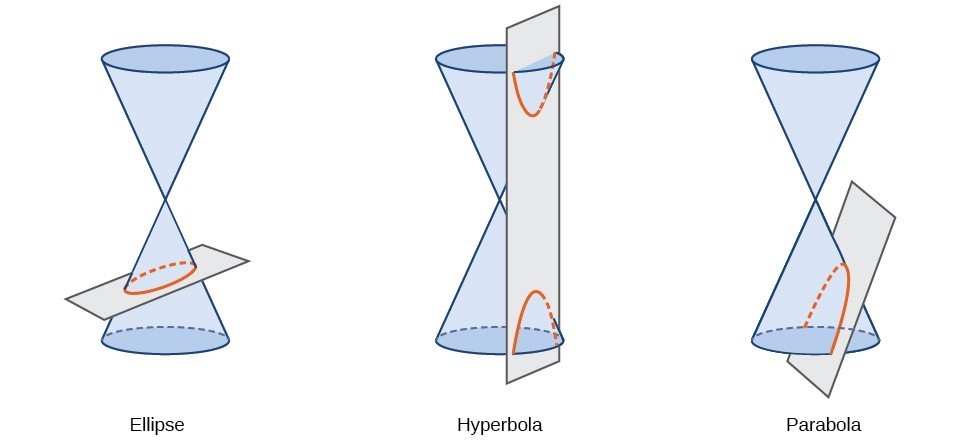
Konische Abschnitte können auch durch einen Satz von Punkten in der Koordinatenebene beschrieben werden. Später in diesem Kapitel werden wir sehen, dass der Graph einer quadratischen Gleichung in zwei Variablen ein Kegelschnitt ist. Die Vorzeichen der Gleichungen und die Koeffizienten der variablen Terme bestimmen die Form. Dieser Abschnitt konzentriert sich auf die vier Variationen der Standardform der Gleichung für die Ellipse. Eine Ellipse ist die Menge aller Punkte \ links (x,y\rechts) in einer Ebene, so dass die Summe ihrer Abstände von zwei festen Punkten eine Konstante ist., Jeder feste Punkt wird als Fokus (Plural: Foci) der Ellipse bezeichnet.
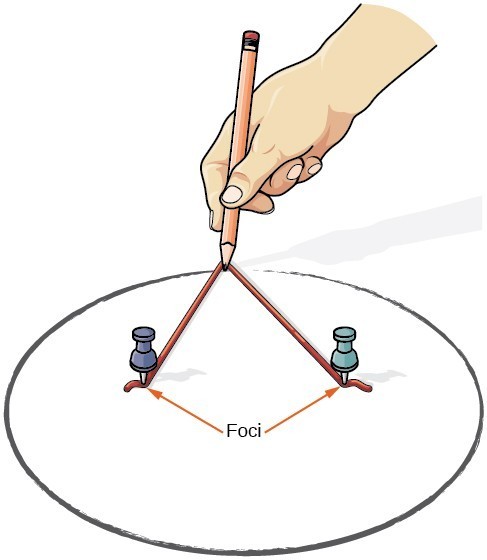
Wir können eine Ellipse mit einem Stück Pappe, zwei Daumenstangen, einem Bleistift und einer Schnur zeichnen. Legen Sie die Daumenblätter in den Karton, um die Herde der Ellipse zu bilden. Schneiden Sie ein Stück Saite länger als den Abstand zwischen den beiden Daumenstapeln (die Länge der Saite stellt die Konstante in der Definition dar). Heften Sie jedes Ende der Saite an die Pappe und zeichnen Sie eine Kurve mit einem Bleistift, der straff gegen die Saite gehalten wird. Das Ergebnis ist eine ellipse.
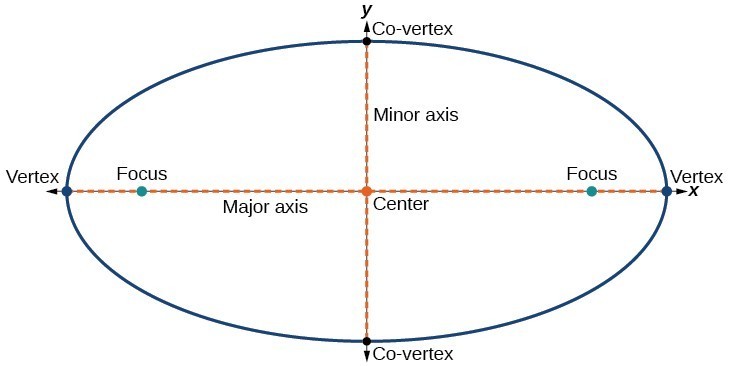
Jede ellipse hat zwei symmetrieachsen., Die längere Achse wird als Hauptachse und die kürzere Achse als Nebenachse bezeichnet. Jeder Endpunkt der Hauptachse ist der Scheitelpunkt der Ellipse (Plural: Scheitelpunkte), und jeder Endpunkt der Nebenachse ist ein Scheitelpunkt der Ellipse. Der Mittelpunkt einer Ellipse ist der Mittelpunkt sowohl der Haupt-als auch der Nebenachse. Die Achsen sind senkrecht in der Mitte. Die Brennpunkte liegen immer auf der Hauptachse, und die Summe der Abstände von den Brennpunkten zu einem beliebigen Punkt auf der Ellipse (die konstante Summe) ist größer als der Abstand zwischen den Brennpunkten.,
In diesem Abschnitt beschränken wir Ellipsen auf solche, die vertikal oder horizontal in der Koordinatenebene positioniert sind. Das heißt, die Achsen liegen entweder auf oder sind parallel zu den x– und y-Achsen. Später im Kapitel sehen wir Ellipsen, die in der Koordinatenebene gedreht werden.
Um mit horizontalen und vertikalen Ellipsen in der Koordinatenebene zu arbeiten, betrachten wir zwei Fälle: diejenigen, die am Ursprung zentriert sind, und diejenigen, die an einem anderen Punkt als dem Ursprung zentriert sind., Zuerst lernen wir, die Gleichungen von Ellipsen abzuleiten, und dann lernen wir, die Gleichungen von Ellipsen in Standardform zu schreiben. Später werden wir verwenden, was wir lernen, um die Diagramme zu zeichnen.,v>Wenn (x,y) ein Punkt auf der Ellipse ist, können wir die folgenden Variablen definieren:
\begin{align}d_1&=\text{der Abstand von } (-c,0) \text{ zu } (x,y) \\ d_2&= \text{der Abstand von } (c,0) \text{ to } (x,y) \end{align}
\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1
für eine Ellipse zentriert am Ursprung mit seiner Hauptachse auf der X-Achse und
\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1
für eine am Ursprung zentrierte Ellipse mit ihrer Hauptachse auf der Y-Achse.,
Schreiben von Gleichungen von Ellipsen,die nicht am Ursprung zentriert sind
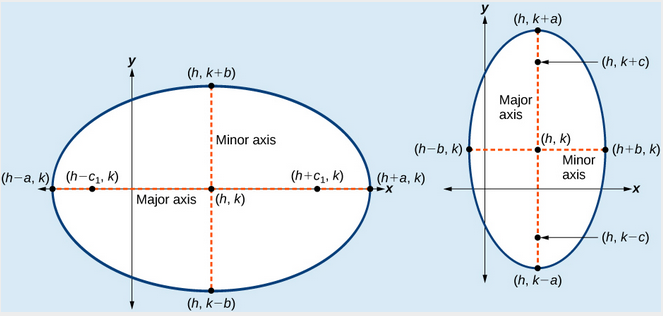
(a) Horizontale Ellipse mit Mitte \links(h,k\rechts) (b) Vertikale Ellipse mit Mitte \links(h, k\rechts)
Lösen angewandter Probleme mit Ellipsen
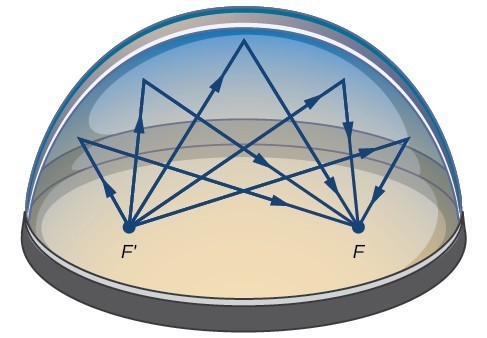
Viele reale Situationen können dargestellt durch Ellipsen, einschließlich Umlaufbahnen von Planeten, Satelliten, Monden und Kometen, und Formen von Bootskielen, Rudern und einigen Flugzeugflügeln. Ein medizinisches Gerät namens Lithotripter verwendet elliptische Reflektoren, um Nierensteine durch Erzeugung von Schallwellen aufzubrechen., Einige Gebäude, Whispering Chambers genannt, sind mit elliptischen Kuppeln so gestaltet, dass eine Person, die bei einem Fokus flüstert, leicht von jemandem gehört werden kann, der bei dem anderen Fokus steht. Dies geschieht aufgrund der akustischen Eigenschaften einer Ellipse. Wenn eine Schallwelle an einem Fokus einer Flüsterkammer entsteht, wird die Schallwelle von der elliptischen Kuppel und zurück zum anderen Fokus reflektiert. In der Flüsterkammer des Museums für Wissenschaft und Industrie in Chicago können sich zwei Personen, die an den Brennpunkten stehen—etwa 43 Fuß voneinander entfernt—flüstern hören.