Dies ist die erste in einer Drei-Post-Serie. Der zweite Beitrag spricht überdie Berechnung von Big-O. Der dritte Artikel spricht über das verstehenDie formale Definition von Big-O.
Big-O-Notation war für mich ein wirklich beängstigendes Konzept. Ich dachte, so sprachen „echte“ Programmierer über ihren Code. Es war alles themore beängstigend, weil die akademischen Beschreibungen (wie Wikipedia) madevery wenig Sinn für mich. Das ist frustrierend, weil die underlyingconcepts eigentlich nicht so schwer sind.,
Einfach ausgedrückt, Big-O-Notation ist, wie Programmierer sprechenalgorithmen. Algorithmen sind ein weiteres beängstigendes Thema, das ich in einem anderen Beitrag behandeln werde, aber für unsere Zwecke sagen wir, dass „Algorithmus“ eine Funktion in Ihrem Programm bedeutet (was nicht zu weit entfernt ist). Die Big-Onotation einer Funktion wird dadurch bestimmt, wie sie auf verschiedene Eingaben reagiert. Wie viel langsamer ist es, wenn wir ihm eine Liste von 1000 Dingen geben, an denen er arbeiten soll, anstelle einer Liste von 1 Ding?
Betrachten Sie diesen Code:
def item_in_list(to_check, the_list): for item in the_list: if to_check == item: return True return False
Wenn wir diese Funktion also wie item_in_list(2, ), sollte es ziemlich schnell sein., Wir durchlaufen jedes Ding in der Liste und wenn wir findendas erste Argument für unsere Funktion gibt True zurück. Wenn wir zum Ende kommenund wir haben es nicht gefunden, gib False zurück.
Die „Komplexität“dieser Funktion ist O(n). Ich werde erklären, was diesbedeutet in nur einer Sekunde, aber lassen Sie uns diese mathematicalsyntax aufschlüsseln. O(n) wird“ Order of N“gelesen, da die O Funktion auch als Order Funktion bekannt ist. Ich denke, das liegt daran, dass wir tunapproximation, die sich mit „Größenordnungen“befasst.,
„Größenordnungen“ ist EIN WEITERER mathematischer Begriff, derbasisch den Unterschied zwischen Zahlenklassen erzählt. Denken Sie an die Differenz zwischen 10 und 100. Wenn Sie sich 10 Ihrer engsten Freunde und 100 Personen vorstellen, ist das ein wirklich großer Unterschied. In ähnlicher Weise ist die Differenz zwischen 1,000 und 10,000 ziemlich groß (in der Tat ist es die Differenz zwischen einem Junker-Auto und einem leicht benutzten). Es stellt sich heraus, dass in Näherung, solange Sie innerhalb einer Größenordnung sind, Sie sind ziemlich nah., Wenn Sie die Anzahl der Gumballs in Amachine erraten würden, wären Sie innerhalb einer Größenordnung, wenn Sie 200gumballs sagen würden. 10.000 Gumballs wären WEIT weg.

Abbildung 1: Ein Gummiballautomat, dessen Anzahl der Gummibälle wahrscheinlich innerhalb einer Größenordnung von 200 liegt.
Zurück zum Sezieren O(n) Dies besagt, dass, wenn wir die Zeit grafisch darstellen würden, die zum Ausführen dieser Funktion mit Eingaben unterschiedlicher Größe erforderlich ist (z. B. Anarray von 1 Element, 2 Elementen, 3 Elementen usw.), wir sehen würden, dass dies ungefähr der Anzahl der Elemente im Array entspricht., Dies wird als linearer Graph bezeichnet. Dies bedeutet, dass die Linie im Grunde gerade ist, wenn Sie sie grafisch darstellen möchten.
Einige von Ihnen haben vielleicht bemerkt, dass unser Code reallyfast wäre, wenn ouritem im obigen Codebeispiel immer das erste Element in der Liste wäre! Das ist wahr, aber bei Big-O dreht sich alles um die ungefähre Worst-Caseperformance, etwas zu tun. Der schlimmste Fall für den obigen Code istdass das, wonach wir suchen, überhaupt nicht in der Liste ist. (Hinweis: Der mathematische Begriff dafür ist „Obergrenze“, was bedeutet, dass es umdie mathematische Grenze der Schrecklichkeit geht.),
Wenn Sie ein Diagramm für diese Funktionen sehen möchten, ignorieren Sie die Funktion O()und ändern die Variable n für x. Sie können dann das in Wolfram Alpha als „plot x“ eingeben, das Ihnen eine Diagonalline zeigt. Der Grund, warum Sie n gegen x austauschen, ist, dass ihr Grafikprogramm x als Variablennamen verwendet, da es der xaxis entspricht. Die x-Achse, die von links nach rechts größer wird, entspricht immer größeren Arrays Ihrer Funktion., Die y-Axis stellt die Zeit dar, also je höher die Linie, desto langsamer ist sie.
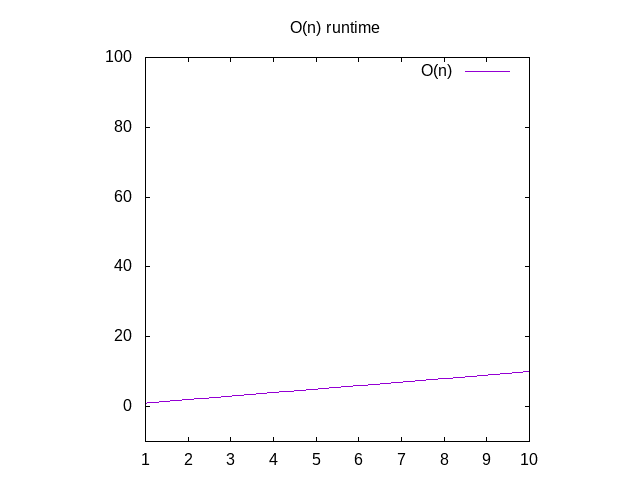
Abbildung 2: Laufzeiteigenschaften einer O(n) – Funktion
Was sind einige andere Beispiele dafür?
Betrachten Sie diese Funktion:
def is_none(item): return item is None
Dies ist ein albernes Beispiel, aber ertragen Sie es mit mir. Diese Funktion istgenannt O(1) was“konstante Zeit“ genannt wird. Was dies bedeutet, ist nomatter, wie groß unsere Eingabe ist, es dauert immer die gleiche Menge an Zeitum die Dinge zu berechnen., Wenn Sie zurück zu Wolfram und plot 1, werden Sie sehendass es immer gleich bleibt, egal wie weit wir gehen. Wenn Sie eine Liste mit 1 Million Ganzzahlen übergeben, dauert es ungefähr die gleiche Zeit, als würden Sie eine Liste mit 1 Ganzzahl übergeben. Konstante Zeit isconsidered das best-case-Szenario für eine Funktion.
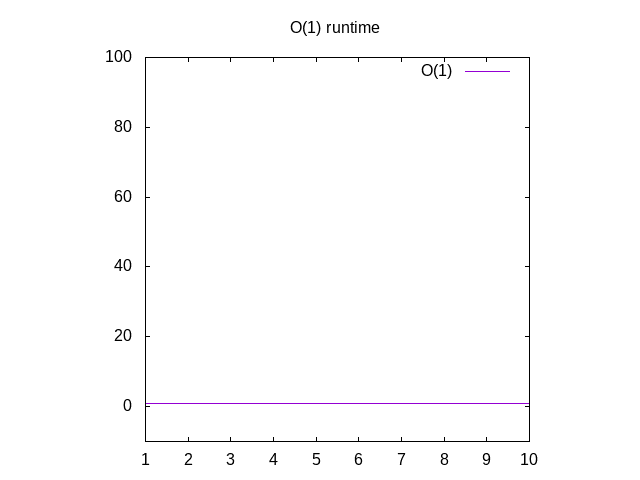
Abbildung 3: Laufzeiteigenschaften einer O(1) – Funktion
Betrachten Sie diese Funktion:
Nachfolgend finden Sie einen Vergleich dieser Diagramme als Referenz., Sie können sehen, dass eine O(n^2) – Funktion sehr schnell langsam wird, da etwas, das in konstanter Zeit arbeitet, viel besser ist. Dies ist besonders nützlich, wenn es um Datenstrukturen geht, über die ich bald schreiben werde.
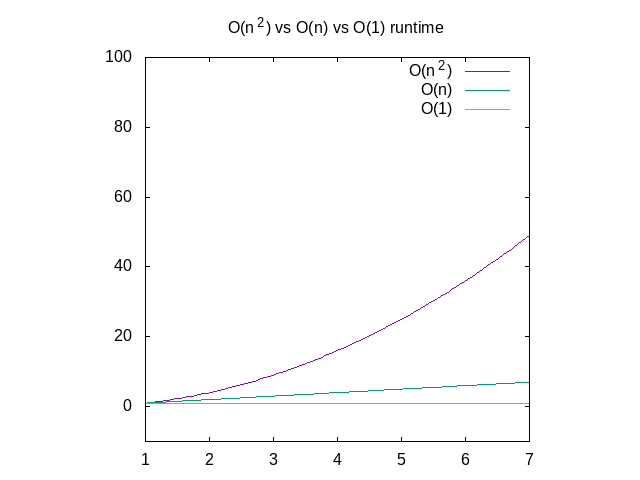
Abbildung 4: Vergleich von O(n2) vs O(n) vs O(1) Funktionen
Dies ist ein ziemlich hoher Überblick über die Big-O-Notation, aber hoffnungsvollvergessen Sie, sich mit dem Thema vertraut zu machen., Es gibt einen Kursera-Kurs, der Ihnen einen tieferen Einblick in dieses Thema geben kann, aber seien Sie gewarnt, dasses sehr schnell in die mathematische Notation springen wird. Wenn hier irgendetwas keinen Sinn ergibt, sende mir eine E-Mail.
Update: Ich habe auch darüber geschrieben, wie man Big-O berechnet
Ich denke darüber nach, ein Buch zu diesem Thema zu schreiben. Wenn dies etwas istSie möchten sehen, bitte äußern Sie Ihr Interesse daran hier.