Wir denken klassisch an Licht wie immer in geraden Linien, aber wenn Lichtwellen in der Nähe einer Barriere passieren, neigen sie dazu, sich um diese Barriere zu biegen und sich auszubreiten. Die Lichtbeugung tritt auf, wenn eine Lichtwelle an einer Ecke oder durch eine Öffnung oder einen Schlitz vorbeikommt, die physikalisch die ungefähre Größe von oder sogar kleiner als die Wellenlänge dieses Lichts ist.,

Eine sehr einfache Demonstration der Beugung kann durchgeführt werden, indem Sie Ihre Hand vor eine Lichtquelle halten und langsam zwei Finger schließen, während Sie das zwischen ihnen übertragene Licht beobachten. Wenn sich die Finger einander nähern und sehr nahe beieinander liegen, sehen Sie eine Reihe dunkler Linien parallel zu den Fingern. Die parallelen Linien sind eigentlich Beugungsmuster. Dieses Phänomen kann auch auftreten, wenn Licht um Partikel „gebogen“ wird, die sich in der gleichen Größenordnung wie die Wellenlänge des Lichts befinden., Ein gutes Beispiel dafür ist die Beugung des Sonnenlichts durch Wolken, die wir oft als Silberstreifen bezeichnen, dargestellt in Abbildung 1 mit einem wunderschönen Sonnenuntergang über dem Meer.
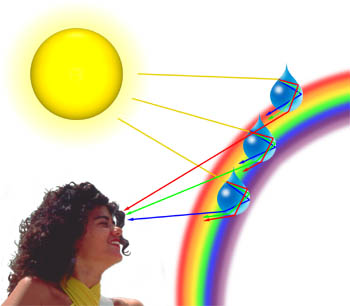
Wir können oft Pastelltöne von Blau, Rosa, Lila und Grün in Wolken beobachten, die erzeugt werden, wenn Licht von Wassertröpfchen in den Wolken gebeugt wird. Die Beugungsmenge hängt von der Wellenlänge des Lichts ab, wobei kürzere Wellenlängen in einem größeren Winkel gebeugt werden als längere (tatsächlich werden blaues und violettes Licht in einem höheren Winkel gebeugt als rotes Licht)., Wenn eine Lichtwelle, die durch die Atmosphäre reist, auf einen Wassertropfen trifft, wie unten dargestellt, wird sie zuerst an der Wasser-Luft-Grenzfläche gebrochen, dann wird sie reflektiert, wenn sie wieder auf die Grenzfläche trifft. Der Strahl, der sich immer noch im Wassertropfen bewegt, wird erneut gebrochen, als er zum dritten Mal auf die Grenzfläche trifft. Diese letzte Wechselwirkung mit der Grenzfläche bricht das Licht zurück in die Atmosphäre, aber es diffundiert auch einen Teil des Lichts, wie unten dargestellt., Dieses Beugungselement führt zu einem Phänomen, das als Cellini-Halo (auch Heiligenschein-Effekt genannt) bekannt ist und bei dem ein heller Lichtring den Schatten des Kopfes des Betrachters umgibt.
Die Begriffe Beugung und Streuung werden oft synonym verwendet und gelten als nahezu synonym. Beugung beschreibt einen speziellen Fall von Lichtstreuung, bei dem ein Objekt mit sich regelmäßig wiederholenden Merkmalen (wie einem Beugungsgitter) eine geordnete Beugung von Licht in einem Beugungsmuster erzeugt., In der realen Welt sind die meisten Objekte in ihrer Form sehr komplex und sollten aus vielen individuellen Beugungsmerkmalen bestehen, die gemeinsam eine zufällige Lichtstreuung erzeugen können.
Eines der klassischen und grundlegendsten Konzepte der Beugung ist das optische Einspalt-Beugungsexperiment, das erstmals im frühen neunzehnten Jahrhundert durchgeführt wurde. Wenn sich eine Lichtwelle durch einen Schlitz (oder eine Öffnung) ausbreitet, hängt das Ergebnis von der physikalischen Größe der Öffnung in Bezug auf die Wellenlänge des einfallenden Strahls ab., Dies wird in Abbildung 3 unter der Annahme veranschaulicht, dass eine kohärente, monochromatische Welle, die von der Punktquelle S emittiert wird, ähnlich wie Licht, das von einem Laser erzeugt würde, durch die Apertur d geht und gebeugt wird, wobei der primäre einfallende Lichtstrahl am Punkt P landet und die erste sekundäre Maxima am Punkt Q auftritt.
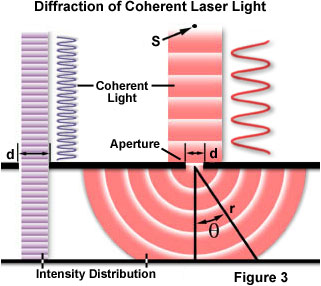
Wie auf der linken Seite der Abbildung gezeigt, wenn die Wellenlänge (λ) viel kleiner als die Aperturbreite (d) ist, bewegt sich die Welle eine gerade Linie, so wie es wäre, wenn es ein Teilchen wäre oder keine Öffnung vorhanden wäre., Wenn jedoch die Wellenlänge die Größe der Blende überschreitet, erleben wir eine Beugung des Lichts gemäß der Gleichung:
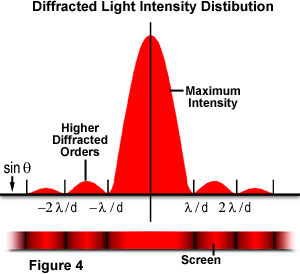
Wobei θ der Winkel zwischen der einfallenden zentralen Ausbreitungsrichtung und dem ersten Minimum des Beugungsmusters ist. Das Experiment erzeugt ein helles zentrales Maximum, das auf beiden Seiten von sekundären Maxima flankiert wird, wobei die Intensität jedes nachfolgenden sekundären Maximums mit zunehmender Entfernung vom Zentrum abnimmt. Abbildung 4 veranschaulicht diesen Punkt mit einem Diagramm der Strahlintensität im Vergleich zum Beugungsradius., Beachten Sie, dass sich die zwischen sekundären Maxima auftretenden Minima in Vielfachen von π befinden.
Dieses Experiment wurde zuerst von Augustin Fresnel erklärt, der zusammen mit Thomas Young wichtige Beweise dafür lieferte, dass Licht in Wellen wandert. Aus den obigen Abbildungen sehen wir, wie ein kohärentes, monochromatisches Licht (in diesem Beispiel Laserbeleuchtung), das von Punkt L emittiert wird, durch Blende d gebeugt wird., Fresnel nahm an, dass die Amplitude der Maxima erster Ordnung am Punkt Q (definiert als eQ) durch die Gleichung gegeben wäre:
wobei A die Amplitude der einfallenden Welle ist, r der Abstand zwischen d und Q ist und f(χ) eine Funktion von χ ist, einem von Fresnel eingeführten Neigungsfaktor.
Lichtbeugung
Erforschen Sie, wie ein Lichtstrahl gebeugt wird, wenn er durch einen schmalen Schlitz oder eine Öffnung geht. Passen Sie die Wellenlänge und Blendengröße an und beobachten Sie, wie sich dies auf das Beugungsintensitätsmuster auswirkt.,
Die Lichtbeugung spielt eine vorrangige Rolle bei der Begrenzung der Auflösungsleistung eines optischen Instruments (z. B. Kameras, Ferngläser, Teleskope, Mikroskope und das Auge). Die Auflösungsleistung ist die Fähigkeit des optischen Instruments, separate Bilder von zwei benachbarten Punkten zu erzeugen. Dies wird häufig durch die Qualität der Linsen und Spiegel im Instrument sowie die Eigenschaften des umgebenden Mediums (normalerweise Luft) bestimmt. Die wellenartige Natur des Lichts erzwingt eine ultimative Grenze für die Auflösungskraft aller optischen Instrumente.,
Unsere Diskussionen über Beugung haben einen Schlitz als Blende verwendet, durch die Licht gebeugt wird. Alle optischen Instrumente haben jedoch kreisförmige Öffnungen, beispielsweise die Pupille eines Auges oder die kreisförmige Membran und Linsen eines Mikroskops. Kreisförmige Öffnungen erzeugen Beugungsmuster, die denen oben beschriebenen ähnlich sind, außer dass das Muster natürlich eine kreisförmige Symmetrie aufweist. Die mathematische Analyse der Beugungsmuster, die durch eine kreisförmige Öffnung erzeugt werden, wird durch die Gleichung beschrieben:
wobei θ (1) die Winkelposition der Beugungsminima erster Ordnung (der erste dunkle Ring) ist, λ die Wellenlänge des einfallenden Lichts ist, d der Durchmesser der Öffnung ist und 1.22 eine Konstante ist. Unter den meisten Umständen ist der Winkel θ (1) sehr klein, so dass die Annäherung, dass die sin und tan des Winkels fast gleich Ausbeuten:
Aus diesen Gleichungen wird ersichtlich, dass das zentrale Maximum direkt proportional zu λ/d ist, wodurch dieses Maximum für längere Wellenlängen und für kleinere Öffnungen stärker ausgebreitet wird., Die sekundäre Nachahmung der Beugung begrenzt die nützliche Vergrößerung von Objektivlinsen in der optischen Mikroskopie aufgrund der inhärenten Lichtbeugung durch diese Linsen. Egal wie perfekt das Objektiv auch sein mag, das Bild einer von der Linse erzeugten Punktlichtquelle wird von Maxima zweiter und höherer Ordnung begleitet. Dies könnte nur beseitigt werden, wenn die Linse einen unendlichen Durchmesser hätte. Zwei Objekte, die durch einen Abstand von weniger als θ(1) getrennt sind, können nicht aufgelöst werden, unabhängig davon, wie hoch die Vergrößerungsleistung ist., Während diese Gleichungen für das Bild einer Punktlichtquelle einen unendlichen Abstand von der Blende abgeleitet wurden, ist es eine vernünftige Annäherung an die Auflösungsleistung eines Mikroskops, wenn d für den Durchmesser der Objektivlinse ersetzt wird.
Wenn also zwei Objekte einen Abstand D voneinander haben und sich in einem Abstand L von einem Beobachter befinden, ist der Winkel (ausgedrückt in Bogenmaß) zwischen ihnen:
was dazu führt, dass wir die letzten beiden Gleichungen kondensieren können, um zu ergeben:
Wobei D(0) der minimale Trennabstand zwischen den Objekten ist, mit dem sie aufgelöst werden können. Mit dieser Gleichung kann das menschliche Auge Objekte lösen, die durch einen Abstand von 0,056 Millimetern getrennt sind, jedoch sind die Photorezeptoren in der Netzhaut nicht nahe genug zusammen, um diesen Auflösungsgrad zu ermöglichen, und 0,1 Millimeter sind unter normalen Umständen eine realistischere Zahl.
Die Auflösungsleistung optischer Mikroskope wird durch eine Reihe von Faktoren bestimmt, einschließlich der diskutierten, aber unter den idealsten Umständen beträgt diese Zahl etwa 0,2 Mikrometer., Diese Zahl muss die optische Ausrichtung des Mikroskops, die Qualität der Linsen sowie die vorherrschenden Lichtwellenlängen berücksichtigen, die zum Abbilden der Probe verwendet werden. Obwohl es oft nicht notwendig ist, die genaue Auflösungsleistung jedes Objektivs zu berechnen (und in den meisten Fällen Zeitverschwendung wäre), ist es wichtig, die Fähigkeiten der Mikroskoplinsen so zu verstehen, wie sie für die reale Welt gelten.
Autoren
Mortimer Abramowitz – Olympus America, Inc., Zwei Corporate Center-Laufwerk., Melville, New York 11747.
Michael W., Davidson – National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.