FRANK K. MCKINNEY
DAS ALTER von Fossilien fasziniert fast jeden. Die Schüler wollen nicht nur wissen, wie alt ein Fossil ist, sondern auch, wie dieses Alter bestimmt wurde. Einige sehr einfache Prinzipien werden verwendet, um das Alter von Fossilien zu bestimmen. Die Schüler sollten in der Lage sein, die Prinzipien zu verstehen und dies als Hintergrund zu haben, damit Altersbestimmungen von Paläontologen und Geologen nicht wie schwarze Magie erscheinen.
Es gibt zwei Arten von Altersbestimmungen., Jahrhunderts untersuchten Gesteinsschichten und die darin enthaltenen Fossilien, um das relative Alter zu bestimmen. William Smith war einer der wichtigsten Wissenschaftler aus dieser Zeit, der dazu beitrug, Kenntnisse über die Abfolge verschiedener Fossilien zu entwickeln, indem er deren Verteilung durch die Abfolge von Sedimentgesteinen in Südengland untersuchte. Jahrhundert hatten sich genügend Informationen über die Rate des radioaktiven Zerfalls angesammelt, dass das Alter von Gesteinen und Fossilien in der Anzahl der Jahre durch radiometrisches Alter bestimmt werden konnte Dating.,
Diese Aktivität zur Bestimmung des Alters von Gesteinen und Fossilien richtet sich an Schüler der 8.oder 9. Klasse. Es wird geschätzt, dass vier Stunden Unterrichtszeit erforderlich sind, einschließlich etwa einer Stunde gelegentlichem Unterricht und Erklärungen des Lehrers und zwei Stunden Gruppen – (Team -) und Einzelaktivitäten der Schüler sowie einer Stunde Diskussion unter den Schülern innerhalb der Arbeitsgruppen.,
Entdecken Sie diesen Link für weitere Informationen zu den in dieser Lektion behandelten Themen:
- Geologische Zeit
ZWECK UND ZIELE
Diese Aktivität hilft den Schülern, die Grundprinzipien zur Bestimmung des Alters von Gesteinen und Fossilien besser zu verstehen. Diese Aktivität besteht aus mehreren teilen. Ziele dieser Aktivität sind:
1) Die Schüler das relative Alter eines geologisch komplexen Gebiets bestimmen zu lassen.
2), um die Schüler mit dem Konzept der Halbwertszeit im radioaktiven Zerfall vertraut zu machen.,
3) Um die Schüler sehen zu lassen, dass einzelne Läufe statistischer Prozesse weniger vorhersehbar sind als der Durchschnitt vieler Läufe (oder dass Läufe mit relativ kleinen Zahlen weniger zuverlässig sind als Läufe mit vielen Zahlen).
4) Zu demonstrieren, wie die Rate des radioaktiven Zerfalls und der Aufbau des resultierenden Zerfallsprodukts in der radiometrischen Datierung von Gesteinen verwendet wird.
5) Verwendung der radiometrischen Datierung und der Prinzipien der Bestimmung des relativen Alters, um zu zeigen, wie das Alter von Gesteinen und Fossilien verengt werden kann, auch wenn sie nicht radiometrisch datiert werden können.,
 Zurück nach oben
Zurück nach oben
BENÖTIGTE MATERIALIEN FÜR JEDE GRUPPE
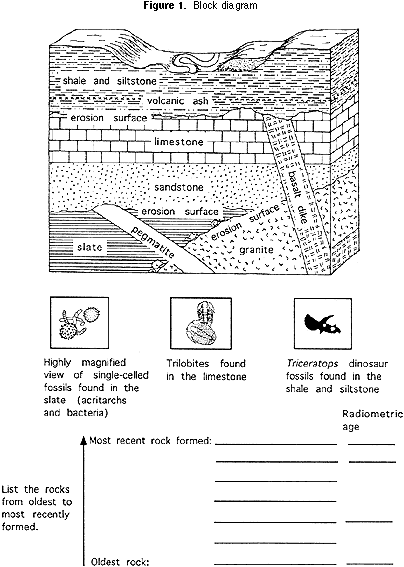
1) Blockdiagramm (Abbildung 1).
2) Großer Becher oder anderer Behälter, in dem M M ‚ s geschüttelt werden können.
3) 100 M M ‚ s
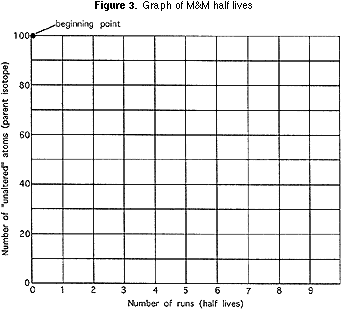
4) Graphenpapier (Abbildung 2).
5) Uhr oder Uhr, die Zeit bis Sekunden hält. (Eine einzelne Uhr oder Uhr für die gesamte Klasse reicht aus.)
6) Stück Papier markiert ZEIT und zeigt entweder 2, 4, 6, 8 oder 10 Minuten.,
7) 128 kleine Karten oder Knöpfe, die aus Pappe oder Konstruktionspapier geschnitten werden können, vorzugsweise mit einer anderen Farbe auf gegenüberliegenden Seiten, die jeweils mit „U-235“ auf einer farbigen Seite und „Pb-207“ auf der gegenüberliegenden Seite markiert sind, die eine Kontrastfarbe aufweist.,
 Zurück nach oben
Zurück nach oben
TEIL 1: BESTIMMUNG DES RELATIVEN ALTERS DER STEINE
Jedes Team von 3 bis 5 Schülern sollte gemeinsam besprechen, wie das relative Alter DER Steine bestimmt werden kann von jeder der Gesteinseinheiten im Blockdiagramm (Abbildung 1). Nachdem die Schüler beschlossen haben, das relative Alter jeder Gesteinseinheit festzulegen, sollten sie sie unter dem Block auflisten, von zuletzt oben in der Liste bis zum ältesten unten.,
Der Lehrer sollte den Schülern mitteilen, dass es zwei Grundprinzipien gibt, die von Geologen verwendet werden, um die Reihenfolge des Steinalters zu bestimmen. Sie sind:
Prinzip der Überlagerung: Jüngere Sedimentgesteine werden auf älteren Sedimentgesteinen abgelagert.
Prinzip der Querschnittsbeziehungen: Jedes geologische Merkmal ist jünger als alles andere, dass es schneidet über.
TEIL 2: RADIOMETRISCHE ALTERSDATIERUNG
Einige Elemente haben Formen (sogenannte Isotope) mit instabilen Atomkernen, dieeine Tendenz zur Veränderung oder zum Zerfall haben., Zum Beispiel ist U-235 ein instabiles Isotop Vonuran, das 92 Protonen und 143 Neutronen in den Nukl eus jedes Atoms hat. Durcheine Reihe von Veränderungen im Kern emittiert es mehrere Teilchenmit 82 Protonen und 125 Neutronen. Dies ist ein stabiler Zustand, und es gibteine weitere Veränderungen im Atomkern. Ein Kern mit dieser Anzahl von Protonenwird Blei genannt (chemisches Symbol Pb). Die Protonen (82) und Neutronen (125) summieren sich. Diese besondere Form (Isotop) von Blei wird Pb-207 genannt. U-235 ist das Parentisotop von Pb-207, dem Tochterisotop.,
Viele Gesteine enthalten kleine Mengen instabiler Isotope und die Tochterisotope, in die sie zerfallen. Wo die Mengen an Eltern – und Tochterisotopen genau gemessen werden können, kann das Verhältnis verwendet werden, um zu bestimmen, wie alt das Gestein ist, wie in den folgenden Aktivitäten gezeigt.
Teil 2a Aktivität-In jedem Moment besteht eine geringe Chance, dass jeder der Kerne von U-235 plötzlich zerfällt. Diese Chance des Verfalls ist sehr gering, aber es ist immer vorhanden und es ändert sich nie. Mit anderen Worten, die Kerne „verschleißen“ nicht oder werden „müde“., Wenn der Kern noch nicht verfallen ist, besteht immer die gleiche, geringe Chance, dass er sich in naher Zukunft ändert.
Atomkerne werden durch eine Anziehungskraft zwischen den großen Kernteilchen (Protonen und Neutronen), die als „starke Kernkraft“ bekannt ist, zusammengehalten, die die elektrostatische Abstoßung zwischen den Protonen innerhalb des Kerns überschreiten muss., Im Allgemeinen muss mit Ausnahme des einzelnen Protons, das den Kern des am häufigsten vorkommenden Wasserstoffisotops bildet, die Anzahl der Neutronen mindestens der Anzahl der Protonen in einem Atomkern entsprechen, da die elektrostatische Abstoßung eine dichtere Verpackung von Protonen verbietet. Wenn jedoch zu viele Neutronen vorhanden sind, ist der Kern möglicherweise instabil und der Zerfall kann ausgelöst werden. Dies geschieht zu jeder Zeit, wenn die Zugabe der flüchtigen „schwachen Kernkraft“ zur allgegenwärtigen elektrostatischen Abstoßung die Bindungsenergie übersteigt, die erforderlich ist, um den Kern zusammenzuhalten.,
Sehr sorgfältige Messungen in Laboratorien, die an einer SEHR GROßEN Anzahl von U-235-Atomen durchgeführt wurden, haben gezeigt, dass jedes der Atome in etwa 704.000.000 Jahren eine Wahrscheinlichkeit von 50:50 aufweist. Mit anderen Worten, während 704 Millionen Jahren wird die Hälfte der zu Beginn dieser Zeit existierenden U-235-Atome zu Pb-207 zerfallen. Dies ist bekannt als die Halbwertszeit von U-235. Viele Elemente haben einige Isotope, die instabil sind, im Wesentlichen, weil sie zu viele Neutronen haben, um durch die Anzahl der Protonen im Kern ausgeglichen zu werden. Jedes dieser instabilen Isotope hat seine eigene charakteristische Halbwertszeit., Einige Halbwertszeiten sind mehrere Milliarden Jahre lang und andere sind so kurz wie eine zehntausendstel Sekunde. Zurück nach oben
Zurück nach oben
Eine schmackhafte Möglichkeit für Schüler, die Halbwertszeit zu verstehen, besteht darin, jedem Team 100 Stück“ regulärer“M M Süßigkeiten zu geben. Auf einem Stück Notizbuchpapier sollte jedes Stück mit dem gedruckten M nach unten gelegt werden. Dies stellt das übergeordnete Isotop dar., Die Süßigkeiten sollten in einen Behälter gegossen werden, der groß genug ist, damit sie frei herumspringen können, sie sollten gründlich geschüttelt und dann wieder auf das Papier gegossen werden, so dass es ausgebreitet wird, anstatt einen Stapel zu bilden. Dieses erste Mal des Schüttelns stellt eine Halbwertszeit dar, und all die Süßigkeiten, die das gedruckte M nach oben haben, stellen eine Veränderung des Tochterisotops dar. Das Team sollte abholen und beiseite legen nur die Stücke von Süßigkeiten, die die M nach oben haben. Zählen Sie dann die Anzahl der verbleibenden Bonbon-Stücke mit dem M nach unten., Dies sind die Elternisotope, die sich während der ersten Halbwertszeit nicht verändert haben.
Der Lehrer sollte jedes Team berichten lassen, wie viele Teile des Elternisotops noch vorhanden sind, und die erste Zeile der Zerfallstabelle (Abbildung 2) sollte ausgefüllt und die durchschnittliche Anzahl berechnet werden. Das gleiche Verfahren zum Schütteln, Zählen der „Überlebenden“ und Ausfüllen der nächsten Zeile auf dem Zerfallstisch sollte noch sieben oder acht Mal durchgeführt werden. Jedes Mal steht für eine Halbwertszeit.
Nachdem die Ergebnisse der letzten „Halbwertszeit“ der M M gesammelt wurden, werden die Bonbons nicht mehr benötigt.,
Jedes Team sollte in einem Diagramm (Abbildung 3) die Anzahl der verbleibenden Bonbon-Stücke nach jedem ihrer „Shakes“ darstellen und jeden aufeinanderfolgenden Punkt im Diagramm mit einer Lichtlinie verbinden. In derselben Grafik sollte jedes Team die DURCHSCHNITTSWERTE für die gesamte Klasse darstellen und diese durch eine schwerere Linie verbinden. UND in derselben Grafik sollte jede Gruppe Punkte zeichnen, bei denen nach jedem „Schütteln“ die Startnummer durch genau zwei geteilt wird, und diese Punkte durch eine unterschiedlich farbige Linie verbinden. (Diese Linie beginnt bei 100; der nächste Punkt ist 100 / 2 oder 50; der nächste Punkt ist 50/2 oder 25; und so weiter.,)
 Nachdem die Diagramme aufgetragen wurden, sollte der Lehrer die Klasse dazu bringen, darüber nachzudenken:
Nachdem die Diagramme aufgetragen wurden, sollte der Lehrer die Klasse dazu bringen, darüber nachzudenken:
1) Warum hat nicht jede Gruppe die gleichen Ergebnisse erzielt?
2) Was folgt der mathematisch berechneten Linie besser? Sind es die Ergebnisse der einzelnen Gruppe oder ist es die Linie, die auf dem Klassendurchschnitt basiert? Warum?
3) Hatten die Schüler eine einfachere Zeit erraten (Vorhersage) die Ergebnisse, wenn es eine Menge Stücke von Süßigkeiten in der Tasse waren, oder wenn es sehr wenige waren? Warum?
U-235 ist in den meisten magmatischen Gesteinen., Wenn das Gestein nicht auf eine sehr hohe Temperatur erhitzt wird, verbleiben sowohl das U-235 als auch seine Tochter Pb-207 im Gestein. Ein Geologe kann den Anteil von U-235-Atomen mit Pb-207 vergleichen und das Alter des Gesteins bestimmen. Der nächste Teil dieser Übung zeigt, wie dies gemacht wird. Zurück nach oben
Zurück nach oben
Teil 2b Aktivität Jedes Team erhält 128 flache Stücke, mit U-235 auf der einen Seite geschrieben und Pb-207 auf der anderen Seite geschrieben. Jedes Team erhält ein Stück Papier markierte ZEIT, auf der entweder 2, 4, 6, 8 oder 10 Minuten geschrieben wird.,
Das Team sollte jedes markierte Stück so platzieren, dass „U-235“ angezeigt wird. Dies stellt Uran-235 dar, das beim Zerfall zu Blei-207 (Pb-207) eine Reihe von Partikeln aus dem Kern emittiert. Wenn jedes Team mit den 128 Teilen fertig ist, die alle „U-235“ zeigen, sollte ein zeitgesteuertes zweiminütiges Intervall beginnen. Während dieser Zeit dreht jedes Team die Hälfte der U-235-Teile um, so dass sie jetzt Pb-207 zeigen. Dies stellt eine „Halbwertszeit“ von U-235 dar, was die Zeit ist, in der die Hälfte der Kerne von der Eltern-U-235 zur Tochter-Pb-207 wechseln.
Ein neues zweiminütiges Intervall beginnt., Während dieser Zeit sollte das Team DIE HÄLFTE DER U-235 umdrehen, DIE NACH DEM ERSTEN ZEITINTERVALL ÜBRIG WAR. Fahren Sie durch insgesamt 4 bis 5 zeitgesteuerte Intervalle fort.
Jedes Team sollte jedoch AUFHÖREN, Teile zu dem auf seinen Zeitungspapieren angegebenen Zeitpunkt umzudrehen. Das heißt, jedes Team sollte gemäß seinem Zeitpapier am Ende des ersten Zeitintervalls (2 Minuten) oder am Ende des zweiten Zeitintervalls (4 Minuten) usw. anhalten. Nachdem alle zeitlichen Intervalle eingetreten sind, sollten sich die Teams nach Anweisung des Lehrers untereinander austauschen., Die Aufgabe für jedes Team besteht nun darin, zu bestimmen, wie viele zeitliche Intervalle (dh wie viele Halbwertszeiten) die Stücke, die sie betrachten, erlebt haben.
Die Halbwertszeit von U-235 beträgt 704 Millionen Jahre. Sowohl das Team, das eine Reihe von Stücken umdrehte, als auch das zweite Team, das das Set untersuchte, sollten bestimmen, wie viele Millionen Jahre durch den Anteil der vorhandenen U-235 und Pb-207 repräsentiert werden, Notizen vergleichen und über Unterschiede feilschen, die sie haben., (Richtig, jedes Team muss die Anzahl von Millionen von Jahren bestimmen, die durch das Set repräsentiert werden, das sie selbst umgedreht haben, PLUS die Anzahl von Millionen von Jahren, die durch das Set repräsentiert werden, das ein anderes Team umgedreht hat.)
TEIL 3: die Umsetzung STAMMT, die AUF FELSEN UND FOSSILIEN
Für das Blockschaltbild (Abbildung 1) zu Beginn dieser übung, das Verhältnis von U-235:Pb-207-Atomen in der pegmatite ist 1:1, und Ihr Verhältnis in den Granit ist 1:3. Mit der gleichen Argumentation über Proportionen wie in Teil 2b oben können die Schüler bestimmen, wie alt der Pegmatit und der Granit sind., Sie sollten das Alter des Pegmatit und Granit neben den Namen der Felsen in der Liste unter dem Blockdiagramm schreiben (Abbildung 1).
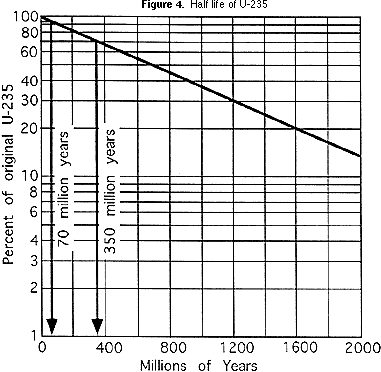
Durch Zeichnen der Halbwertszeit auf einer Art Skala, die als logarithmische Skala bekannt ist, kann die gekrümmte Linie wie die für die MTM-Aktivität M begradigt werden, wie Sie in der Grafik in Abbildung 4 sehen können. Dies macht die Kurve nützlicher, weil es einfacher ist, sie genauer zu zeichnen. Dies ist besonders hilfreich für Verhältnisse von Elternisotop zu Tochterisotop, die weniger als eine Halbwertszeit darstellen., Wenn für das Blockdiagramm (Abbildung 1) ein geochemisches Labor feststellt, dass die Vulkanasche im Schlickstein ein Verhältnis von U-235:Pb-207 von 47:3 aufweist (94% der ursprünglichen U-235-Reste), bedeutet dies, dass die Asche 70 Millionen Jahre alt ist (siehe Abbildung 4). Wenn das Verhältnis im Basalt 7:3 beträgt (70% des ursprünglichen U-235 verbleiben), ist der Basalt 350 Millionen Jahre alt (siehe Abbildung 4). Die Schüler sollten das Alter der Vulkanasche neben dem Schiefer schreiben, Schlickstein und Basalt auf der Liste unter dem Blockdiagramm., Zurück nach oben
Zurück nach oben
FRAGEN ZUR DISKUSSION
1) Können Sie anhand des verfügbaren radiometrischen Alters das mögliche Alter der Gesteinseinheit mit Acritarchen und Bakterien bestimmen? Was ist das? Warum kannst du nicht genau sagen, wie alt der Felsen ist?
2) Können Sie das mögliche Alter der Gesteinseinheit bestimmen, die Trilobiten hat? Was ist das? Warum kannst du nicht genau sagen, wie alt der Felsen ist?
3) Was ist das Alter des Gesteins, das die Triceratops Fossilien enthält?, Warum können Sie das Alter dieses Felsens genauer bestimmen als das Alter des Felsens mit den Trilobiten und des Felsens, der Acritarchen und Bakterien enthält?
Hinweis für Lehrer: Basierend auf Querschnittsbeziehungen wurde festgestellt, dass der Pegmatit jünger als der Schiefer ist und dass der Schiefer jünger als der Granit ist. Daher ist der Schiefer, der den Acritarch und Bakterien enthält, zwischen 704 Millionen Jahren und 1408 Millionen Jahren alt, weil der Pegmatit 704 Millionen Jahre alt ist und der Granit 1408 Millionen Jahre alt ist., Der Schiefer selbst kann nicht radiometrisch datiert werden, kann also nur zwischen dem Alter des Granits und dem Pegmatit eingeklammert werden.
Der trilobithaltige Kalkstein überlagert den Quarzsandstein, der den Pegmatit kreuzt, und der Basalt durchschneidet den Kalkstein. Daher müssen die Trilobiten und das Gestein, das sie enthält, jünger als 704 Millionen Jahre (das Alter des Pegmatiten) und älter als 350 Millionen Jahre (das Alter des Basaltes) sein. Der Kalkstein selbst kann nicht radiometrisch datiert werden, kann also nur zwischen dem Alter des Granits und dem Pegmatit eingeklammert werden.,
Die Triceratops-Dinosaurierfossilien sind ungefähr 70 Millionen Jahre alt, da sie in Schiefer und Schlickstein vorkommen, die Vulkanasche enthalten, die radiometrisch auf 70 Millionen Jahre datiert ist. Alle unter der Vulkanasche gefundenen Triceratops können etwas älter als 70 Millionen Jahre sein, und alle oben gefundenen können etwas jünger als 70 Millionen Jahre sein., Das Alter der Triceratops kann genauer bestimmt werden als das der Acritarchen und Bakterien und das der Trilobiten, da die Gesteinseinheit, die die Triceratops enthält, selbst radiometrisch datiert werden kann, während das der anderen Fossilien dies nicht konnte.