Widerstände vs. Induktivitäten
Induktivitäten verhalten sich nicht die gleiche weise wie widerstände tun. Während Widerstände einfach dem Stromfluss durch sie entgegenwirken (indem sie eine Spannung fallen lassen, die direkt proportional zum Strom ist), widersetzen sich Induktivitäten Stromänderungen durch sie, indem sie eine Spannung fallen lassen, die direkt proportional zur Stromänderungsrate ist.
Nach dem Lenzschen Gesetz ist diese induzierte Spannung immer so polar, dass versucht wird, den Strom auf seinem gegenwärtigen Wert zu halten., Das heißt, wenn der Strom an Größe zunimmt, „drückt“ die induzierte Spannung gegen den Stromfluss; Wenn der Strom abnimmt, kehrt sich die Polarität um und „drückt“ den Strom, um sich der Abnahme zu widersetzen.
Dieser Widerstand gegen die aktuelle Veränderung wird eher als Reaktanz als als Widerstand bezeichnet., Mathematisch ausgedrückt ist die Beziehung zwischen der über den Induktor fallenden Spannung und der Stromänderungsrate durch den Induktor wie folgt:

Wechselstrom in einem einfachen induktiven Stromkreis
Der Ausdruck di/dt ist einer aus dem Kalkül, dh die Änderungsrate des Momentanstroms (i) im Laufe der Zeit in Ampere pro Sekunde.
Die Induktivität (L) ist in Henrys, und die momentane Spannung (e) ist natürlich in Volt., Manchmal finden Sie die Rate der momentanen Spannung ausgedrückt als „v“ anstelle von „e“ (v = L di/dt), aber es bedeutet genau das gleiche.
Um zu zeigen, was mit Wechselstrom passiert, analysieren wir eine einfache Induktorschaltung:
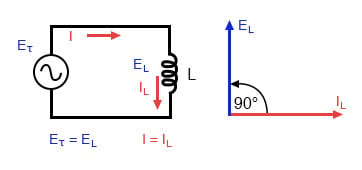
Reine induktive Schaltung: Induktorstrom verzögert Induktorspannung um 90°.
Wenn wir den Strom und die Spannung für diese sehr einfache Schaltung zeichnen würden, würde es ungefähr so aussehen:

Reine induktive Schaltung, Wellenformen.,
Denken Sie daran, dass die Spannung, die über einen Induktor fällt, eine Reaktion gegen die Änderung des Stroms durch ihn ist.
Daher, die momentane spannung ist null, wenn die momentane strom ist an einer spitze (null ändern, oder ebene steigung, auf die aktuelle sinus welle), und die momentane spannung ist an einer spitze, wo die momentane strom ist bei maximale ändern (die punkte der steilsten steigung auf die aktuelle welle, wo es kreuzt die null linie).
Dies führt zu einer Spannungswelle, die 90° außerhalb der Phase mit der Stromwelle liegt., Betrachtet man den Graphen, scheint die Spannungswelle einen „Vorsprung“ auf der Stromwelle zu haben; Die Spannung „führt“ den Strom und der Strom „bleibt“ hinter der Spannung zurück.

Strom lags spannung durch 90° in eine reine induktive schaltung.
Die Dinge werden noch interessanter, wenn wir die Leistung für diese Schaltung zeichnen:

In einer reinen induktiven Schaltung kann die momentane Leistung positiv oder negativ sein.,
Weil momentane power ist das produkt der momentanen spannung und die momentane strom (p=dh), die leistung gleich null, wenn die momentane strom oder spannung ist null. Immer wenn der Momentanstrom und die Spannung beide positiv sind (über der Leitung), ist die Leistung positiv.
Wie beim Widerstandsbeispiel ist auch die Leistung positiv, wenn der Momentanstrom und die Spannung beide negativ sind (unterhalb der Leitung).,
Da die Strom – und Spannungswellen jedoch 90° außerhalb der Phase liegen, gibt es Zeiten, in denen eine positiv ist, während die andere negativ ist, was zu ebenso häufigen Vorkommen negativer Momentanleistung führt.
Was ist negative Leistung?
Aber was bedeutet negative Leistung? Dies bedeutet, dass der Induktor die Energie an den Stromkreis zurückgibt, während eine positive Leistung bedeutet, dass er die Energie aus dem Stromkreis absorbiert.,
Da die positiven und negativen Leistungszyklen im Laufe der Zeit in Größe und Dauer gleich sind, gibt der Induktor genauso viel Strom an den Stromkreis zurück, wie er über den Zeitraum eines vollständigen Zyklus absorbiert.
Dies bedeutet im praktischen Sinne, dass die Reaktanz eines Induktors die Nettoenergie von Null ableitet, ganz im Gegensatz zum Widerstand eines Widerstands, der Energie in Form von Wärme ableitet. Wohlgemerkt, dies ist nur für perfekte Induktivitäten, die keinen Drahtwiderstand haben.
Reaktanz vs., Widerstand
Der Widerstand eines Induktors gegen eine Stromänderung führt im Allgemeinen zu einem Widerstand gegen Wechselstrom, der sich definitionsgemäß immer in momentaner Größe und Richtung ändert.
Dieser Widerstand gegen Wechselstrom ähnelt dem Widerstand, unterscheidet sich jedoch dadurch, dass er immer zu einer Phasenverschiebung zwischen Strom und Spannung führt und keine Leistung ableitet. Aufgrund der Unterschiede hat es einen anderen Namen: Reactance. Die Reaktanz zu AC wird in Ohm ausgedrückt, genau wie der Widerstand, mit der Ausnahme, dass sein mathematisches Symbol X anstelle von R ist.,
Um genau zu sein, wird die mit einem Induktor verbundene Reaktanz normalerweise durch den Großbuchstaben X mit einem Buchstaben L als Index symbolisiert: XL.
Da Induktivitäten die Spannung proportional zur Rate der Stromänderung abfallen lassen, fallen sie mehr Spannung für sich schneller ändernde Ströme und weniger Spannung für sich langsamer ändernde Ströme. Dies bedeutet, dass die Reaktanz in Ohm für jeden Induktor direkt proportional zur Frequenz des Wechselstroms ist., Die genaue Formel zur Bestimmung der Reaktanz lautet wie folgt:

Wenn wir einen 10-mH-Induktor Frequenzen von 60, 120 und 2500 Hz aussetzen, werden die Reaktanzen in der folgenden Tabelle angezeigt.
Reaktanz eines 10 mH Induktors:
| Frequenz (Hertz) | Reaktanz (Ohm) |
| 60 | 3.7699 |
| 120 | 7.5398 |
| 2500 | 157.,0796 |
In der Blindwiderstand Gleichung, die der Begriff „2nf“ (alles auf der rechten Seite, außer die L) hat eine Besondere Bedeutung für sich. Es ist die Anzahl der Radiant pro Sekunde, bei der sich der Wechselstrom „dreht“, wenn Sie sich einen Wechselstromzyklus vorstellen, um die Drehung eines vollen Kreises darzustellen.
Ein Radiant ist eine Einheit der Winkelmessung: Es gibt 2π Radiant in einem vollen Kreis, so wie es 360° in einem vollen Kreis gibt., Wenn der Generator, der den Wechselstrom erzeugt, eine zweipolige Einheit ist, erzeugt er einen Zyklus für jede volle Umdrehung der Wellenrotation, dh alle 2π Radiant oder 360°.
Wenn diese Konstante von 2π mit der Frequenz in Hertz (Zyklen pro Sekunde) multipliziert wird, ergibt sich eine Zahl in Bogenmaß pro Sekunde, die als Winkelgeschwindigkeit des Wechselstromsystems bezeichnet wird.
Winkelgeschwindigkeit in AC-Systemen
Winkelgeschwindigkeit kann durch den Ausdruck 2nf oder durch ein eigenes Symbol dargestellt werden, den griechischen Kleinbuchstaben omega, der unserem römischen Kleinbuchstaben „w“ ähnlich erscheint: ω., Somit könnte die Reaktanzformel XL = 2nfL auch als XL = wL geschrieben werden.
Es muss verstanden werden, dass diese „Winkelgeschwindigkeit“ ein Ausdruck dafür ist, wie schnell die AC-Wellenformen radfahren, wobei ein Vollzyklus gleich 2π Radiant ist. Es ist nicht unbedingt repräsentativ für die tatsächliche Wellengeschwindigkeit des Generators, der den Wechselstrom erzeugt.
Wenn der Generator mehr als zwei Pole hat, ist die Winkelgeschwindigkeit ein Vielfaches der Wellengeschwindigkeit., Aus diesem Grund wird ω manchmal in Einheiten elektrischer Radiant pro Sekunde und nicht in (einfachen) Radiant pro Sekunde ausgedrückt, um es von mechanischer Bewegung zu unterscheiden.
In irgendeiner Weise drücken wir die Winkelgeschwindigkeit des Systems aus, es ist offensichtlich, dass es direkt proportional zur Reaktanz in einem Induktor ist. Wenn die Frequenz (oder Generatorwellendrehzahl) in einem Wechselstromsystem erhöht wird, bietet eine Induktivität einen größeren Widerstand gegen den Stromfluss und umgekehrt.,
Der Wechselstrom in einem einfachen induktiven Stromkreis ist gleich der Spannung (in Volt) geteilt durch die induktive Reaktanz (in Ohm), ebenso wie der Wechsel-oder Gleichstrom in einem einfachen resistiven Stromkreis gleich der Spannung (in Volt) geteilt durch den Widerstand (in Ohm) ist. Eine Beispielschaltung wird hier gezeigt:

Induktive Reaktanz

Phasenwinkel
Wir müssen jedoch bedenken, dass Spannung und Strom hier nicht in Phase sind., Wie bereits gezeigt, hat die Spannung eine Phasenverschiebung von +90° in Bezug auf den Strom. Wenn wir diese Phasenwinkel von Spannung und Strom mathematisch in Form komplexer Zahlen darstellen, stellen wir fest, dass der Widerstand eines Induktors gegen Strom auch einen Phasenwinkel hat:


Strom verzögert Spannung um 90° in einem Induktor.
Mathematisch sagen wir, dass der Phasenwinkel des Stromwiderstands eines Induktors 90° beträgt, was bedeutet, dass der Stromwiderstand eines Induktors eine positive imaginäre Größe ist., Dieser Phasenwinkel des reaktiven Stromwiderstands wird in der Schaltungsanalyse von entscheidender Bedeutung, insbesondere für komplexe Wechselstromkreise, in denen Reaktanz und Widerstand interagieren.
Es wird sich als vorteilhaft erweisen, den Widerstand einer Komponente gegen Strom in Bezug auf komplexe Zahlen und nicht skalare Widerstands-und Reaktanzgrößen darzustellen.
REVIEW:
- Induktive Reaktanz ist der Gegensatz, den ein Induktor aufgrund seiner phasenverschobenen Speicherung und Freisetzung von Energie in seinem Magnetfeld zu Wechselstrom bietet., Die Reaktanz wird durch den Großbuchstaben „X“ symbolisiert und wie der Widerstand (R) in Ohm gemessen.Die induktive Reaktanz
- kann mit dieser Formel berechnet werden: XL = 2nfL
- Die Winkelgeschwindigkeit eines Wechselstromkreises ist eine weitere Möglichkeit, seine Frequenz in Einheiten elektrischer Radiant pro Sekunde anstelle von Zyklen pro Sekunde auszudrücken. Es wird durch den griechischen Kleinbuchstaben „omega“ oder ω symbolisiert.
- Die induktive Reaktanz nimmt mit zunehmender Frequenz zu. Mit anderen Worten, je höher die Frequenz ist, desto mehr widersetzt sie sich dem Wechselstromfluss von Elektronen.,
VERWANDTE ARBEITSBLÄTTER:
- Induktivitäten Arbeitsblatt
- Induktive Reaktanz Arbeitsblatt